/ Accueil / Arithmétique / Nombres congruents

Triangles rectangles rationnels – Nombres congruents – Courbes elliptiques


En septembre 2009 une équipe de chercheurs d'Amérique du Nord, d'Europe, d'Australie et d'Afrique du Sud, a calculé plus de mille milliards de nombres congruents (1012). C'est plus une prouesse technique que théorique, en effet tant qu'une conjecture de Birch et Swinnerton-Dyer n'est pas prouvée, on ne peut affirmer que tous les nombres calculés sont congruents. Les principales propriétés utilisées sont connues depuis des années (Lire par exemple l'article Courbes elliptiques de John Coates dans le Leçons de mathématiques d'aujourd'hui). Les résultats permettent de mieux connaître les nombres congruents et en particulier leur répartition.
Dans cette page, avec un peu de patience, vous en calculerez cent mille = 105 ou pas beaucoup plus, toujours sous réserve que la même conjecture soit démontrée, mais vous aurez réellement sous les yeux tous ces nombres congruents !

105 = 100000 nombres congruents. Les 100 000 premiers nombres congruents sans facteurs carrés congruentsE5.zip ou congruentsE5.txt.gz (230 K). (Calculs effectués à l'aide du programme qui accompagne cette page).
106 = 1000000 nombres congruents. Le premier million = 106 = 1000 000 de nombres congruents sans facteurs carrés (suite OEIS A006991 Primitive congruent numbers) fichier .zip ou fichier .gz (2.4 M environ). 
5, 6, 7, 13, 14, 15, 21, 22, 23, 29, 30, 31, 34, 37, 38, 39, 41, 46, 47, 53, 55, 61, 62, 65, 69, 70, 
71, 77, 78, 79, 85, 86, 87, 93, 94, 95, 101, 102, 103, 109, 110, 111, 118, 119, 127, 133, 134, 137, 
138, 141, 142, 143, 145, 149, 151, 154, 157, 158, 159, 161, 165, 166, 167, 173, 174, 181, 182, 183, 
190, 191, 194, 197, 199, 205, 206, 210, 213, 214, 215, 219, 221, 222, 223, 226, 229, 230, 231, 237, ...

Le premier million de nombres congruents avec ou sans facteurs carrés (suite OEIS A003273) est fichier .zip ou fichier .gz (2.15 M environ). 
5 6 7 13 14 15 20 21 22 23 24 28 29 30 31 34 37 38 39 41 45 46 47 52 53 54 55 56 60 61 62 63 65 69 70 
71 77 78 79 80 84 85 86 87 88 92 93 94 95 96 101 102 103 109 110 111 112 116 117 118 119 120 124 125 
126 127 133 134 135 136 137 138 141 142 143 145 148 149 150 151 152 154 156 157 158 159 161 164 165 
166 167 173 174 175 180 181 182 183 184 188 189 190 191 194 197 198 199 205 ...

Description

Pythagore : Le triangle ABC est rectangle en A si et seulement si AB2 + AC2 = BC2.

D'après le théorème de Pythagore et sa réciproque, un triangle ABC est rectangle en A si et seulement si AB2 + AC2 = BC2. Le côté BC est l'hypoténuse du triangle, les deux autres AB et AC sont les côtés de l'angle droit.

triangle rectangle ABC

En notant AB=b, AC=a, BC=c, la relation s'écrit a2 + b2 = c2 ou encore c = racine(a2 + b2).
Les grecs on pu inventer les nombres irrationnels à l'aide de ce théorème (la racine carrée de 2 comme diagonale d'un carré de côté 1, par exemple).

Généralement donc les longueurs a, b et c sont des nombres réels positifs quelconques.
Le triangle ABC dont les côtés sont les entiers a=AB=3, b=AC=4, c=BC=5 est bien connu et sert parfois à construire des angles droits. Ce triangle (3, 4, 5) est dit triangle pythagoricien.
Triangle pythagoricien (3, 4, 5)

Définitions

Triangles pythagoriciens (a, b, c)

Un triangle pythagoricien est un triangle rectangle dont les trois côtés (a, b, c) sont des entiers.

Les coordonnées (a, b)des points placés sur la figure ci-dessus sont les valeurs des côtés de l'angle droit d'un triangle rectangle pythagoricien (lorsque a et b inférieurs à 200), l'hypoténuse c est la distance du point à l'origine du repère.
On obtient tous les triangles pythagoriciens de côtés premiers entre eux, en prenant a=2xy, b=x^2-y^2 et c = x2+y2 et en faisant varier x et y premiers entre eux, (x>y>0). (a est le petit côté pair, b le petit côté impair et c le grand côté, c'est-à-dire l'hypoténuse du triangle rectangle).
faq

Un triangle rectangle rationnel est un triangle rectangle dont les trois côtés sont des rationnels.

Les triangles pythagoriciens sont des cas particuliers de triangles rationnels. En réduisant au même dénominateur d les côtés (a/d, b/d, c/d) d'un triangle rationnel, on obtient un triangle pythagoricient (a, b, c) à côtés entiers. En multipliant ou en divisant les trois côtés (r, s, t) d'un triangle rationnel par un même nombre rationnel q on obtient encore un triangle rationnel (rq, sq, tq) ou (r/q, s/q, t/q) selon le cas. Par exemple (3, 4, 5) et (1/2, 2/3, 5/6) en divisant par 6.

Un entier naturel non nul D est dit congruent s'il est l'aire d'un triangle rectangle rationnel.

a, b, c rationnels non nuls, c=racine(a2+ b2) et D = ab/2 entier naturel

triangle rectangle rationnel

Exemples

6 est congruent, en effet le triangle (3, 4, 5) est rectangle et rationnel d'aire 6=3×4/2 est rationnel.
5 est congruent, en effet (9/6, 40/6, 41/6) est un triangle rectangle rationnel d'aire 9×40/(36×2) = 5. (Voir la page sur Fibonacci).
1 n'est pas congruent (Fermat). La suite des nombres congruents est la suite A003273 de N. J. A. Sloane.
Nombres congruents inférieurs à 10000

Historique

 — Des problèmes similaires se trouvent dans les écrits de Diophante (210 - 290). Ensuite les nombres congruents apparaissent dans les travaux du Perse al-Karaji (953-1029) qui pose le problème de trouver un entier n et un rationnel r tels que r2 - n et r2 + n soient aussi des carrés (ces trois carrés sont alors en progression arithmétique). Par exemple, en se restreignant à r entier, ces carrés peuvent être 1, 25, 49 et n=24 ou encore 9, 225, 441 et n=216. Le nombre n est alors le quadruple de ce qu'on appelle actuellement un nombre congruent (les trois carrés sont congruents modulo n, d'où le nom de nombre congruent donné autrefois à à n, cf. ci-dessous).
Soient a et b tels que r2-n=(a-b)2 et r2+n=(a+b)2, en soustrayant membre à membre et en divisant par 2 on obtient n=2ab alors qu'en additionnant on obtient r2=a2+b2, ce qui montre que n/4 est un nombre congruent selon la définition actuelle. (Il y a relativement peu de temps encore, en 1964, au chapitre II du livre Elementary Theory of Numbers de Sierpinski, c'est n qui correspond à la définition d'un nombre congruent. Vous trouverez tous les détails des calculs dans ce livre en ligne.)

 — À Pise en 1225, le même problème fut posé par Théodore et Jean de Palerme dans un tournoi mathématique organisé par Frédérique II. Fibonacci montre que 5 et 7 sont des nombres congruents, donne une solution r=41/12 lorsque n=5 et affirme sans démonstration que que 1 n'est pas congruent. Fibonacci montre aussi que l'aire d'un triangle pythagoricien est divisible par 6. Pour n entier non nul, n<5, il n'y a pas de solution où r2 ± n sont des carrés.
En 1931; J.D. Hill donne pour n=5 la solution r=3344161/1494696, depuis Uspensky et Heaslet on donné d'autres solutions dans lesquelles numérateur et dénominateur ont 15 chiffres et une formule avec paramétre qui permet de calculer une infinité de solutions : x2+5y2=z2, x2-5y2=t2, n=(x4+25y4)/(2xyzt).

 — En 1659, Pierre de Fermat démontre que 1 n'est pas congruent. Il est équivalent de dire que l'aire d'un triangle rationnel ne peut pas être un carré, ce qui revient à dire qu'un nombre congruent n'est pas un carré

 — En 1915, le statut des nombres jusqu'à 100 est connu. En 1980 il reste encore des nombres inférieurs à 1000 dont on ne sait s'ils sont congruents ou non.

 — En 1952 Kurt Heegner montre en introduisant des techniques nouvelles et profondes, que tous les nombres premiers de la suite arithmétique 5, 13, 21, 29 ... sont congruents.

 — En 1975 Nelson Stephens établit un lien entre les nombres congruents et la conjecture de Birch et Swinnerton-Dyer (Un prix d'un million de dollars est offert par le "Clay Math Institute" à qui résoudra Cette conjecture) .

 — En 1982 Jerrold Tunnell exploite le lien avec les courbes elliptiques précédemment utilisé par Heegner. Il trouve une formule simple qui permet de savoir si un nombre est ou non congruent . (Cette formule est exploitée dans cette page). Toutefois la formule ne permet de dire qu'un entier est congruent que sous condition de la validité de la conjecture de Birch et Swinnerton-Dyer.

 — 2009 Plus de mille milliards de nombres congruents.

Calculez un nombre congruent

1) Choisissez deux nombres x et y, alors a=2xy, b=x^2-y^2 et c = x2+y2 sont les côtés d'un triangle rectangle pythagoricien.
(Ces trois formules à deux paramètres x et y permet de générer tous les triangles pythagoriciens).
2) L'aire de ce triangle est ab/2 = xy(x2-y2)
3) En divisant par pgcd et facteurs carrés adéquats, on simplifie et on obtient les valeurs ci-dessous :

Entrez x et y          



En faisant varier x de 2 à et en prenant y inférieur à x , plusieurs nombres congruents (ceux-ci sont réordonnés).



Mais il n'est pas évident de prouver que 157 est congruent car le triangle rectangle le plus simple d'aire 157 a pour côtés a = 6803298487826435051217540/411340519227716149383203, b = 411340519227716149383203/21666555693714761309610, c = 224403517704336969924557513090674863160948472041/8912332268928859588025535178967163570016480830

Théorème de Tunnell

Un nombre entier est dit sans facteur carré s'il n'est pas divisible par le carré d'un entier (autre que 1).
Par exemple 2, 3, 5, 6, 7, 10, 11 sont sans facteurs carrés alors que 4, 8, 9, 12=3*4 ne le sont pas.

En 1982 l'Américain Jerrold Tunnell a obtenu un critère simple de détermination des nombres congruents, sous réserve qu'une certaine conjecture soit démontrée.

Soient An, Bn, Cn, Dn,les nombres de solutions d'équations définis ci-dessous
An = |{x,y,z) ∈ Z3 / n=2x2+y2+32z2}|
Bn = |{x,y,z) ∈ Z3 / n=2x2+y2+8z2}|
Cn = |{x,y,z) ∈ Z3 / n=8x2+2y2+64z2}|
Dn = |{x,y,z) ∈ Z3 / n=8x2+2y2+16z2}|

Si n est congruent, impair et sans facteur carré, alors 2An = Bn,
si n est congruent, pair et sans facteur carré, alors 2Cn = Dn.
Réciproquement, si la conjecture de Birch et Swinnerton-Dyer s'applique aux courbes elliptiques de la forme y2 = x3 - n2x, alors les égalités ci-dessus suffisent pour que n soit congruent (n étant sans facteur carré, pair ou impair selon l'égalité utilisée)

Calcul des nombres congruents sans facteurs carrés, jusqu'à N

Pour N pas trop grand (ci-dessous, on peut aller jusqu'à N=300000 pour 101131 congruents), en faisant varier x, y, z, il est facile de dénombrer pour n ≤ N tous les nombres de solutions An, Bn, Cn, Dn et donc de déterminer les nombres congruents sans facteurs carrés (sous réserve que la conjecture de Birch et Swinnerton-Dyer soit vraie).

Calcul des nombres congruents sans facteurs carrés.

N =   

Courbes elliptiques

Paramétrisation du cercle

La figure ci-dessus représente le cercle unité et le point M variable de ce cercle.
Ce cercle est paramétré par la pente t de la demi-droite AM.
Les expressions des coordonnées (u, v) du point M du cercle sont indiquées sur la figure. Les petits côtés du triangle rectangle sont a/c = u et b/c =v, l'hypoténuse est c/c=1, c'est le rayon du cercle. On peut voir par le calcul que a, b, c sont rationnels si et seulement si t est rationnel
En posant D=ab/2, x = -Dt et y=D2(1+t2)/c, on montre que M est sur le cercle privé de A, si et seulement si y≠0 et y2 = x3 - D2x. On obtient donc la courbe elliptique représentée ci-dessous (D=5 sur la figure).

D est un nombre congruent si et seulement s'il existe un point (x, y) où x et y≠0 sont rationnels, sur la courbe ED d'équation y2 = x3 - D2x.

Exemple : Lorsque a=3/2, b=20/3, c=41/6 et D=5, on obtient u=9/41, v=40/41, t=4/5, x=-4, y=6 et on peut vérifier que le point rationnel (-4, 6) est sur la courbe d'équation y2 = x3 - 25x ainsi d'ailleurs que les deux autres points rationnels (0, 0), (-5, 0) et (5, 0) (qui ne correspondent à aucun triangle rationnel car y=0)
Inversement, connaissant (x, y) on a t=-x/D,   c=D2(1+t2)/y ce qui permet ensuite de calculer a et b à partir des formules de u et de v.

Courbe elliptique


À continuer...

Logiciels et outils disponibles sur le net

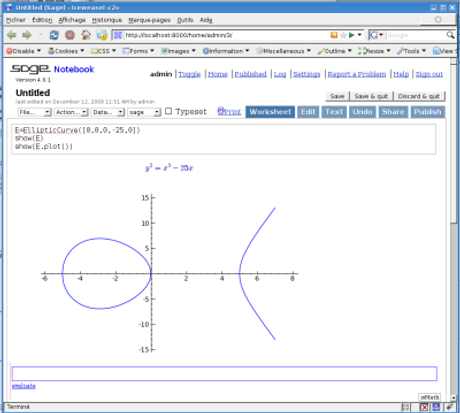
notebook sage mwrank and related programs for elliptic curves over Q par J. E. Cremona, University of Warwick, U.K.
mwrank est un programme écrit en C++ pour calculer les groupes de Mordell-Weil des courbbes elliptiques sur Q. Depuis 2007, mwrank fait partie de la librairie eclib incluse dans Sage. La manière la plus simple d'utiliser mwrank est donc d'installer Sage qui est un environnement très complet et disponible pour de nombreux OS, y compris Ms.W.
Cremona's tables of elliptic curves et The Stein-Watkins table of elliptic curves.
Elliptic Curve Data by J. E. Cremona University of Warwick, U.K. At present the tables contain data for conductors up to 130000. Algorithms for Modular Elliptic Curves Online Edition by J. E. Cremona
Sage est utilisable en "notebook" (image ci-contre) ou comme shell (exemple ci-dessous).
Exemple (retranscription incomplète): 
jp@stang:~$ sage
-------------------------------------------------------------
| Sage Version 4.0.1, Release Date: 2009-06-06              
| Type notebook() for the GUI, and license() for information.
-------------------------------------------------------------
sage: !mwrank
Program mwrank: uses 2-descent (via 2-isogeny if possible) to
determine the rank of an elliptic curve E over Q, and list a
set of points which generate E(Q) modulo 2E(Q).
and finally saturate to obtain generating points on the curve.
...
Enter curve: [0,0,0,-25,0]
Curve [0,0,0,-25,0] :
3 points of order 2:
[-5:0:1], [0:0:1], [5:0:1]

****************************
* Using 2-isogeny number 1 *
****************************
...

PARI/GP is a widely used computer algebra system designed for fast computations in number theory (factorizations, algebraic number theory, elliptic curves...)
NZMATH is a Python based number theory oriented calculation system. It is developed at Tokyo Metropolitan University.
SIMATH is a computer algebra system, especially for number theoretic purpose. Basic algorithms for elliptic curves Horst G. Zimmer
Plusieurs autres logiciels pour la théorie des nombres
GAP - Groups, Algorithms, Programming a System for Computational Discrete Algebra
Maxima, a Computer Algebra System

Compléments, documents, références, liens

Pages de liens sur l'arithmétique, les nombres, le théorème de Fermat, Andrew John Wiles, Pell, Diophante d'Alexandrie.

Les nombres gelés d'Antoine de Saint-Exupéry
Équation de Weierstrass bloc notes (linenn.davalan.eu) – la détermination des nombres à la fois triangulaires et pyramidaux revient à égaler deux polynômes de degrés diffents 2 et 3, l'un d'une variable, l'autre d'une autre variable.
Trois milliards de nombres congruents Par Marie-Neige Cordonnier. – Pour la Science 21/10/2009 – Une nouvelle méthode informatique ouvre les horizons d'un problème mathématique du Xe siècle.
La Recherche Nombres congruents. Le cap des mille milliards est franchi. Par Jean-François Mestre. La Recherche Décembre 2009 N° 438 p. 18
Le plus grand nombre congruent jamais calculé dépasse la barre symbolique des mille milliards. Sa découverte est un exploit technique, mais aussi une confirmation d'anciennes conjectures.
Le problème des nombres congruents PDF par Pierre Colmez Version commentée d'un exposé donné, en mai 2005, au séminaire des élèves de l'École Polytechnique.
Birch and Swinnerton-Dyer conjecture Clay Mathematics Institute - Lecture by Fernando Rodriguez-Villegas and Official Problem by A. Wiles.
A Trillion Triangles   September 22, 2009 -- Mathematicians from North America, Europe, Australia, and South America have resolved the first one trillion cases of an ancient mathematics problem. Press release in MSWord
Pythagorean triples and the congruent number problem   
Introduction élémentaire à la théorie des courbes elliptiques   Marc Joye (UCL 1995/1 Technical Report )
Congruum g : 1 <= g <= 999   Hisanori Mishima
Congruent Numbers PDF Kent E. Morrison (Elliptic Curves, Tunnel's Criterion, The Formula). A Trillion Triangles Détails. Article
Congruum g : 1 <= g <= 999   Congruent Numbers Hisanori Mishima
Elliptic curves and right triangles   Karl Rubin


Dave Rusin 14H52: Elliptic Curves
Le cauchemar du professeur De Koninck Claude Levesque – U. Laval
Diophantine Geometry: An Introduction  de M. Hindry, J.H. Silverman – Diophantine equations are systems of polynomial equations to be solved in integers or rational numbers, and Diophantine geometry is the study of Diophantine equations using... – Springer
Arithmétique  de Marc Hindry – Tableau Noir – Calvage & Mounet
Courbes elliptiques   John Coates – Leçons de mathématiques d'aujourd'hui tome I – 2000 CASSINI
Algèbre arithmétique et maple   Bernadette Perrin-Riou – CASSINI
Cours d'arithmétique  Jean-Pierre Serre Professeur au Collège de France – PUF le mathématicien 1970
Les courbes elliptiques racontées à mes enfants  Conférence de Marc Hindry 28 mai 2008. enregistrement vidéo d'une durée de 90 minutes – IREM
Points rationnels et courbes elliptiques Jérôme Gärtner – Le but de cet article est d'introduire à deux notions utilisées actuellement dans la recherche en théorie des nombres : les points rationnels et les courbes elliptiques. – CultureMATH Ressources pour les enseignants de mathématiques. Site expert des Ecoles Normales Supérieures et du Ministère de l'Education Nationale
Elementary theory of numbers   Waclaw Sierpinski (Warszawa 1964)

Autres documents et exposés pour l'enseignement
Arcs-en-ciel, soucoupes volantes, toupies, courbes elliptiques, et tout ça  Michèle Audin (2004)
Pendules et courbes elliptiques   Rémy Oudompheng (2009)
















Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.

J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.

© (Copyright) Jean-Paul Davalan 2002-2014