/ Accueil / Arithmétique / I Nombres premiers Hyperbole
Crible géométrique utilisant une hyperbole(*)
Description
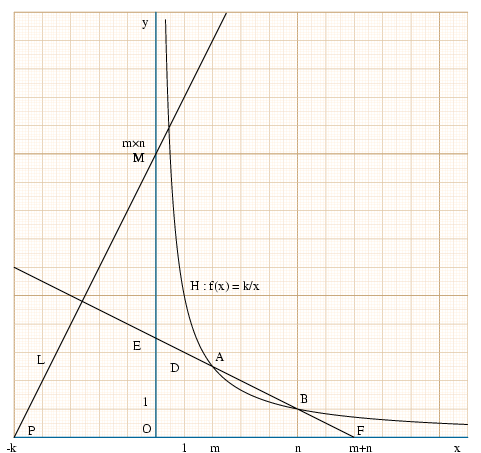
L'hyperbole H d'équation y=k/x est tracée dans un repère orthonormé. Les produits m × n de deux naturels m et n sont obtenus à l'aide d'une règle et d'une équerre.
(m et n pourraient être des réels mais seuls les naturels nous intéressent ici).
Comme application on fera apparaître l'ensemble des nombres premiers sur l'axe vertical du repère.
On trace la droite D = (AB) passant par les deux points A et B d'abscisses respectives m et n de H. (Si m=n, la droite D est tangente à H).
La perpendiculaire L à D, passant par P (-k, 0) coupe l'axe vertical (Oy) en M d'ordonnée m × n.
(m et n pourraient être des réels mais seuls les naturels nous intéressent ici).
Comme application on fera apparaître l'ensemble des nombres premiers sur l'axe vertical du repère.
On trace la droite D = (AB) passant par les deux points A et B d'abscisses respectives m et n de H. (Si m=n, la droite D est tangente à H).
La perpendiculaire L à D, passant par P (-k, 0) coupe l'axe vertical (Oy) en M d'ordonnée m × n.
La démonstration est simple et rapide :
La droite D = (AB) a pour pente (k/n -k/m)/(n-m) = -k/(mn) et donc sa perpendiculaire L a pour pente mn/k.
On en déduit que le point d'intersection M de L et de (Oy) a pour ordonnée mn.
Lorsque toutes les droites L sont tracées pour toutes les valeurs entières de m et n à partir de 2, les nombres premiers sont visibles sur l'axe (Oy), ce sont les points où ne passent aucune droite L.
Crible des nombres premiers
Remarques :
La droite D coupe l'axe (Ox) en un point F d'abscisse m+n. Elle coupe (Oy) en un point E d'ordonnée k(1/m+1/n) = k(m+n)/(mn).
E est l'orthocentre du triangle PMF car (MO) et (AB) sont deux hauteurs, d'où (PE) est orth. à (MF).
On peut aussi utiliser les points A et B d'abscisses -m et n, le principal avantage est de ne pas avoir à tracer de tangente lorsque m = n, contrairement à ce qu'il se passe dans le cas de la parabole où la figure se trouve réduite de moitié, ici elle double de taille : Figure
La droite D = (AB) a pour pente (k/n -k/m)/(n-m) = -k/(mn) et donc sa perpendiculaire L a pour pente mn/k.
On en déduit que le point d'intersection M de L et de (Oy) a pour ordonnée mn.
Lorsque toutes les droites L sont tracées pour toutes les valeurs entières de m et n à partir de 2, les nombres premiers sont visibles sur l'axe (Oy), ce sont les points où ne passent aucune droite L.
Remarques :
La droite D coupe l'axe (Ox) en un point F d'abscisse m+n. Elle coupe (Oy) en un point E d'ordonnée k(1/m+1/n) = k(m+n)/(mn).
E est l'orthocentre du triangle PMF car (MO) et (AB) sont deux hauteurs, d'où (PE) est orth. à (MF).
On peut aussi utiliser les points A et B d'abscisses -m et n, le principal avantage est de ne pas avoir à tracer de tangente lorsque m = n, contrairement à ce qu'il se passe dans le cas de la parabole où la figure se trouve réduite de moitié, ici elle double de taille : Figure
Clin d'oeil au procédé de Yuri Matiiassevitch et Boris Stechkin qui utilisent une parabole.
Liens
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


