Accueil > Mots > Suites > Fibonacci > Fibonacci 9
Suite de Fibonacci
Dans la nature
Les plantes
Pomme de pin
Lorsque vous regardez la pomme de pin, les écailles dessinent naturellement des réseaux de lignes parallèles. On pourrait observer sur la pomme de pin ci-dessous, 5 lignes bleues, 8 rouges et 13 blanches, (seules quelques unes sont dessinées).

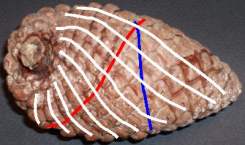
Mise en évidence de 5, 8 ou 13 lignes, suivant la direction choisie.


Mise en évidence de 5, 8 ou 13 lignes, suivant la direction choisie.
Fleurs
Dans le coeur de cette fleur choisie au hasard dans le jardin, on retrouve les deux nombres de Fibonacci consécutifs F(7)=13 et F(8)=21

Cliquez plusieurs fois sur la fleur !
Cliquez sur la marguerite des jardins ci-dessous et comptez les nombres de spirales dans l'un ou l'autre sens, vous devriez retrouver les deux nombres de Fibonacci consécutifs 21 et 34.

Cliquez sur l'image pour voir
le coeur de la marguerite.
Cliquez sur une vignette pour ouvrir les pages contenant de plus grandes images. (2 dahlias, tournesol, souci, ananas, pomme de conifère).















Cliquez plusieurs fois sur la fleur !
Cliquez sur la marguerite des jardins ci-dessous et comptez les nombres de spirales dans l'un ou l'autre sens, vous devriez retrouver les deux nombres de Fibonacci consécutifs 21 et 34.

Cliquez sur l'image pour voir
le coeur de la marguerite.
Cliquez sur une vignette pour ouvrir les pages contenant de plus grandes images. (2 dahlias, tournesol, souci, ananas, pomme de conifère).












Phyllotaxie
Foliation
En botanique la phyllotaxie ou foliation est la disposition des feuilles sur la tige. (d'après Le Petit Larousse).
Par extension la phyllotaxie est aussi la disposition des éléments d'un fruit, d'une fleur, d'un bourgeon ou d'un capitule.
La science qui étudie ces arrangements est aussi appelée phyllotaxie. (Wikipedia - Phyllotaxie).
Par extension la phyllotaxie est aussi la disposition des éléments d'un fruit, d'une fleur, d'un bourgeon ou d'un capitule.
La science qui étudie ces arrangements est aussi appelée phyllotaxie. (Wikipedia - Phyllotaxie).
Spirales
Courbes
Plusieurs modèles de spirales logarithmiques liées à des nombres de Fibonacci consécutifs, comme vous pouvez les observer dans la nature, sont disponibles dans un seul fichier ou séparément. Les fichiers sources en LaTeX utilisent l'extension 'curves' (ce qui explique la forme approximative des spirales logarithmiques).
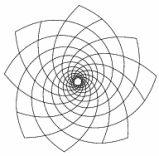


Ces spirales correspondent à des espacements (divergences) de k*137.5077 degrés sur une spirale logarithmique principale non dessinée (voir aussi l'applet ci-dessous).
Comparez l'image de gauche au logo de l'European Mathematical Society (EMS).
| Sens habituel | [3-5] | [5-8] | [8-13] | [13-21] | [21-34] |
| Les symétriques | [3-5] | [5-8] | [8-13] | [13-21] | [21-34] |
| Fleurs | [3-5] | [5-8] | [8-13] | [13-21] | [21-34] |



Ces spirales correspondent à des espacements (divergences) de k*137.5077 degrés sur une spirale logarithmique principale non dessinée (voir aussi l'applet ci-dessous).
Comparez l'image de gauche au logo de l'European Mathematical Society (EMS).






