Suite des nombres de Catalan
Description
Historique
 C'est en dénombrant les décompositions d'un polygone régulier convexe en triangles, par des diagonales non sécantes, que E. Catalan introduit au début du 19e siècle la suite de nombres qui porte maintenant son nom. À la même époque Binet s'intéressa au même problème. Au siècle précédent déjà, Segner (hongrois d'origine germanique) et Euler avaient abordé cete étude.
C'est en dénombrant les décompositions d'un polygone régulier convexe en triangles, par des diagonales non sécantes, que E. Catalan introduit au début du 19e siècle la suite de nombres qui porte maintenant son nom. À la même époque Binet s'intéressa au même problème. Au siècle précédent déjà, Segner (hongrois d'origine germanique) et Euler avaient abordé cete étude.
Le nombre de Catalan Cn donne le nombre de découpages d'un polygone de n+2 côtés en n triangles en traçant n-1 diagonales (lorsque n est au moins égal à 1).
Valeurs
Le début de la suite Cn est 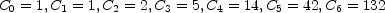 . Cette suite est référencée A000108 dans lencyclopédie de N. J. A. Sloane.
. Cette suite est référencée A000108 dans lencyclopédie de N. J. A. Sloane.
Pour tout n entier naturel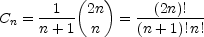
La formule de récurrence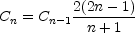 permet de calculer Cn lorsqu'on connaît n et Cn-1 (lorsque n > 0). C'est la méthode de calcul utilisée par l'application javascript ci-dessous.
permet de calculer Cn lorsqu'on connaît n et Cn-1 (lorsque n > 0). C'est la méthode de calcul utilisée par l'application javascript ci-dessous.
La formule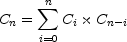 exprime le nombre de Catalan Cn en fonction de tous ses précédents.
exprime le nombre de Catalan Cn en fonction de tous ses précédents.
Par exemple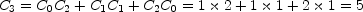 ou encore
ou encore
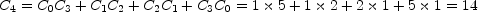
Pour tout n entier naturel
La formule de récurrence
La formule
Par exemple
Application
Quelques suites
Nombres de Catalan
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, 18367353072152, 69533550916004, 263747951750360, 1002242216651368, 3814986502092304, 14544636039226909, 55534064877048198, 212336130412243110, 812944042149730764, 3116285494907301262, 11959798385860453492, 45950804324621742364, 176733862787006701400, 680425371729975800390,Nombres de chiffres des écritures décimales des nombres de Catalan
1, 1, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 9, 9, 10, 10, 11, 11, 12, 13, 13, 14, 14, 15, 16, 16, 17, 17, 18, 18, 19, 20, 20, 21, 21, 22, 23, 23, 24, 24, 25, 25, 26, 27, 27, 28, 28, 29, 30, 30, 31,Nombres de diviseurs premiers
0, 0, 1, 1, 2, 3, 4, 3, 4, 4, 5, 5, 6, 7, 9, 7, 8, 8, 10, 9, 10, 10, 11, 11, 11, 12, 12, 11, 13, 13, 14, 11, 13, 14, 14, 13, 14, 14, 16, 15, 16, 18, 19, 19, 19, 19, 21, 19, 20, 19, 21, 20, 21, 21, 21, 19, 20,Nombres de diviseurs
1, 1, 2, 2, 4, 8, 12, 8, 16, 16, 24, 32, 48, 72, 192, 96, 192, 256, 576, 512, 768, 768, 1024, 1152, 1152, 1728, 1536, 1536, 4096, 4096, 5120, 2048, 6144, 12288, 12288, 8192, 12288, 12288, 24576, 24576, 36864, 98304, 131072, 147456, 196608, 196608, 368640, 294912, 442368, 294912, 524288, 393216,
Calculs
Combinatoire
Les nombres de Catalan permettent de dénombrer un grand nombre d'objets mathématiques.
En particulier C(n) est le nombre de
- triangulations de polygones convexes de n+2 sommets à l'aide de n-1 diagonales non sécantes (à l'intérieur du polygone)
- parenthésages binaires de n+1 termes : ((a+b)+c)+(e+f), a+(b+((c+e)+f)) ... C(4)=14
- différents types d'arbres (des graphes) ou de chemins
- chaînes de caractères de toutes sortes ou des suites finies d'entiers
- certains types de permutations
- certains types de partitions
- etc.


