Accueil / Jeux / Jeux Arithmétiques / Carrés gréco-latins
Carrés gréco-latins
Les carrés gréco-latins sont présents sur une autre page du site, sous la forme d'un carré à compléter à l'aide de seize cartes à jouer. Si on avait plus de quatre couleurs carreau, cœur, trèfle, pique, on pourrait construire un puzzle de 25, 49 etc. cartes.
Carrés latins
1 – Prenez un ensemble E de n éléments, par exemple n=5 et E = {a, b, c, d, e}
2 – Prenez un carré C de n × n cases.
3 – Placez les n éléments de E dans les n cases de la première ligne du carré C.
4 – Placez les n éléments de E dans les n cases de la deuxième ligne. Mais attention, chaque élément doit être différent de celui qui est dans la case au-dessus.
– Placez les n éléments de E dans les n cases de la troisième ligne. Chaque élément doit être différent de ceux qui sont dans les cases placées au-dessus.
– Continuez à remplir les lignes, l'une après l'autre. Les éléments de E doivent être présents une fois et une seule sur chaque ligne et une fois et une seule sur chaque colonne.
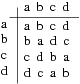
1 – Les lois des groupes donnent des carrés latins (mais les carrés latins ne sont pas tous des groupes comme vous pouvez l'observer ici dans de nombreux cas).
Chaque carré latin obtenu ci-dessus peut être considéré comme une table d'opération (table de Pythagore ou de Cayley) des éléments dans l'ordre alphabétique de E = {a, b, c...}. (Habituellement ils sont placés à gauche et au-dessus du carré).
Les propriétés de cette loi sont indiquées le cas échéant.
(Ces tests sont effectués lorsque vous cliquez sur le bouton [Aléatoire]).
2 – Les sudokus sont des carrés latins d'ordre 9, dont les éléments sont les entiers de 1 à 9. Ils ont une propriété supplémentaire, chacune des neuf boites intérieures contient les éléments de 1 à 9 une fois et une seule chaque. Des livrets à imprimer de grilles de sudokus sont disponibles ici. (Les grilles sont renouvelées automatiquement chaque jour, les solutions sont indiquées en fin de livret).
2 – Prenez un carré C de n × n cases.
3 – Placez les n éléments de E dans les n cases de la première ligne du carré C.
4 – Placez les n éléments de E dans les n cases de la deuxième ligne. Mais attention, chaque élément doit être différent de celui qui est dans la case au-dessus.
– Placez les n éléments de E dans les n cases de la troisième ligne. Chaque élément doit être différent de ceux qui sont dans les cases placées au-dessus.
– Continuez à remplir les lignes, l'une après l'autre. Les éléments de E doivent être présents une fois et une seule sur chaque ligne et une fois et une seule sur chaque colonne.
Exemples

1 – Les lois des groupes donnent des carrés latins (mais les carrés latins ne sont pas tous des groupes comme vous pouvez l'observer ici dans de nombreux cas).
Chaque carré latin obtenu ci-dessus peut être considéré comme une table d'opération (table de Pythagore ou de Cayley) des éléments dans l'ordre alphabétique de E = {a, b, c...}. (Habituellement ils sont placés à gauche et au-dessus du carré).
Les propriétés de cette loi sont indiquées le cas échéant.
(Ces tests sont effectués lorsque vous cliquez sur le bouton [Aléatoire]).
2 – Les sudokus sont des carrés latins d'ordre 9, dont les éléments sont les entiers de 1 à 9. Ils ont une propriété supplémentaire, chacune des neuf boites intérieures contient les éléments de 1 à 9 une fois et une seule chaque. Des livrets à imprimer de grilles de sudokus sont disponibles ici. (Les grilles sont renouvelées automatiquement chaque jour, les solutions sont indiquées en fin de livret).
Carrés latins orthogonaux et carrés gréco-latins
Deux carrés latins A et B de mêmes dimensions n × n sont orthogonaux lorsque vous ne pouvez pas trouver dans deux cases différentes, à la fois les mêmes éléments de A et de B.
Pour tous i, j, u, v, on a A(i, j) ≠ A(u, v) ou B(i, j) ≠ B(u, v)
Il existe pour certaines valeurs de n, des familles de plusieurs carrés latins deux à deux orthogonaux. Lorsqu'il existe un corps fini de n éléments, il existe des familles de n-1 carrés latins deux à deux orthogonaux, leur construction est détaillée plus bas dans cette page.
En juxtaposant les éléments de deux carrés latins orthogonaux A et B dans les cases du même carré C et dans l'ordre A avant B, on obtient un carré gréco-latin dont les éléments sont C(i,j) = A(i, j) B(i, j).
Les deux carrés latins choisis sont orthogonaux si et seulement si le carré C a toutes ses cases différentes.
Pour tous i, j, u, v, on a A(i, j) ≠ A(u, v) ou B(i, j) ≠ B(u, v)
Il existe pour certaines valeurs de n, des familles de plusieurs carrés latins deux à deux orthogonaux. Lorsqu'il existe un corps fini de n éléments, il existe des familles de n-1 carrés latins deux à deux orthogonaux, leur construction est détaillée plus bas dans cette page.
En juxtaposant les éléments de deux carrés latins orthogonaux A et B dans les cases du même carré C et dans l'ordre A avant B, on obtient un carré gréco-latin dont les éléments sont C(i,j) = A(i, j) B(i, j).
Les deux carrés latins choisis sont orthogonaux si et seulement si le carré C a toutes ses cases différentes.
Lettres latines et grecques
La dénomination "carré gréco-latin" vient de l'habitude qu'avait Euler de prendre des lettres grecques pour écrire le carré A et des lettres latines pour le carré B. Les cases du carré C contiennent donc chacune une lettre grecque et une lettre latine.
La lettre grecque d'une case est différente de toutes les autres lettres grecques de sa ligne et de sa colonne. Idem, la lettre latine d'une case est différente de toutes les lettres latines de sa ligne et de sa colonne.
Cliquez ici sur le bouton [ Calcule] pour obtenir un carré gréco-latin et ses lettres grecques et latines.
La lettre grecque d'une case est différente de toutes les autres lettres grecques de sa ligne et de sa colonne. Idem, la lettre latine d'une case est différente de toutes les lettres latines de sa ligne et de sa colonne.
Cliquez ici sur le bouton [ Calcule] pour obtenir un carré gréco-latin et ses lettres grecques et latines.
Deux carrés latins orthogonaux de côtés impairs
Carrés orthogonaux de côtés $n$ impairs, pour $n$ variant de 3 à 21 obtenus par cette méthode : Fichier pdf.
Le côté $n$ et les coefficients $r$ et $s$ doivent être premiers entre eux, on doit aussi avoir "r-s" non nul et premier avec $n$. (Ces conditions ne pourraient pas être respectées si $n$ était pair).
Le côté $n$ et les coefficients $r$ et $s$ doivent être premiers entre eux, on doit aussi avoir "r-s" non nul et premier avec $n$. (Ces conditions ne pourraient pas être respectées si $n$ était pair).
Corps finis
Les corps finis à q éléments (q au moins égal à 2) n'existent que si et seulement si q est de la forme q = pa où p est un naturel premier et où l'exposant a
est un naturel au moins égal à 1. Ces corps sont tous commutatifs.
Deux corps finis ayant un même nombre q d'éléments sont isomorphes. (Ils sont en un certain sens identiques, on passe de l'un à l'autre en permutant les éléments).
Lorsque q = p premier, ce corps est Z/pZ = Zp.
Si vous ne connaissez pas Zp ={0, 1, 2..., p-1}, allez lire le paragraphe du bas de page pour apprendre à additionner ou à multiplier dans Zp.
Les corps Zp pour p premier, sont très simples à construire, celà a été fait dans cette page. Cela n'a pas été réalisé ici pour le moment lorsque q = p2 ou p3 ... ou pα.
Deux corps finis ayant un même nombre q d'éléments sont isomorphes. (Ils sont en un certain sens identiques, on passe de l'un à l'autre en permutant les éléments).
Lorsque q = p premier, ce corps est Z/pZ = Zp.
Si vous ne connaissez pas Zp ={0, 1, 2..., p-1}, allez lire le paragraphe du bas de page pour apprendre à additionner ou à multiplier dans Zp.
Les corps Zp pour p premier, sont très simples à construire, celà a été fait dans cette page. Cela n'a pas été réalisé ici pour le moment lorsque q = p2 ou p3 ... ou pα.
Méthode de construction de carrés gréco-latins à l'aide de propriétés des corps finis
Lorsque
Chaque couple de deux carrés carrés latins orthogonaux, nous donne un carré gréco-latin.
Les éléments
Démonstrations de Bose (1938), Stevens (1939), construction déjà utilisée par E.H. Moore (1896).
Fq est un corps fini à q éléments on construit aisément q-1 carrés latins deux à deux orthogonaux.
Chaque couple de deux carrés carrés latins orthogonaux, nous donne un carré gréco-latin.
Les éléments
ai,j des matrices Ak sont dans Fq,
ai,j = xi × xk + xj lorsque xk n'est pas nul et varie dans Fq.
(Avec xi, xk, xj dans Fq)
Démonstrations de Bose (1938), Stevens (1939), construction déjà utilisée par E.H. Moore (1896).
Corps à p éléments (p premier)
On se place dans le corps

Zp = {1, 2, 3, 4, ..., p-1, 0} où p est un nombre premier.
Corps à q = pa éléments (p premier et a ≥ 1)
On se place dans le corps $F_{p^a} = GF(p^a)$ où $p$ premier et $a\geq 1$, le nombre d'éléments est $q=p^a$.
Vous pouvez construire un grand nombre de tables d'addition et de multiplication de corps finis à la page Corps Finis.
Choisissez le nombre premier $ p $ = 2, 3, 5, 7, ... et l'exposant $ a \geq 1 $, l'application construira un corps de $p^a$ éléments et $p^a-1$ carrés latins deux à deux orthogonaux et affichera autant de carrés que demandés.
Pour que le résultat soit lisible, évitez que $p^a$ dépasse la valeur 100.
Vous pouvez construire un grand nombre de tables d'addition et de multiplication de corps finis à la page Corps Finis.
Choisissez le nombre premier $ p $ = 2, 3, 5, 7, ... et l'exposant $ a \geq 1 $, l'application construira un corps de $p^a$ éléments et $p^a-1$ carrés latins deux à deux orthogonaux et affichera autant de carrés que demandés.
Pour que le résultat soit lisible, évitez que $p^a$ dépasse la valeur 100.
Calculs dans Zp
Pour n > 0, Z/nZ = Zn est pour l'addition, le groupe additif modulo n. Pour l'addition et la multiplication modulo n, c'est un anneau.
Pour ceux qui ne connaissent pas (Zn , +, ×) et qui voudraient tout de même savoir calculer sans passer plus d'une minute à apprendre.
Pour additionner ou multiplier dans Zn, faites exactement comme dans N ou Z, c'est tout ou presque :
si le résultat est aussi grand que n ou plus, divisez-le par n et donnez seulement le reste de la division.
Exemple pour n=5 :
On écrira pour simplifier, l'ensemble Z5 sous la forme Z5 = {0, 1, 2, 3, 4}.
Il n'y a pas d'élément 5 ni no plus au delà. 0 est mis à la place de tous les nombres {0, 5, 10, 15... }. De même 1 est à la place de {1, 6, 11, 16, ...} etc.
Calculez 2+2 = 4, 1+2 = 3 ... c'est simple, puis 3+4 = 12 que l'on écrira plutôt 2, on a donc 3+4 = 2, on a 1+4 = 0 etc. Il en est de même pour la multiplication : 3*4 = 2 (car en divisant 12 par 5, le reste est 2 ou si vous préférez, 12 = 5 + 5 + 2)
Autres exemples:
Dans Z7 6 × 5 = 30 et 30 divisé par 7 a pour reste 2, donc dans Z7 on a 6 × 5 = 2.
(C'est comme dans l'écriture 6 × 5 &equiv 2 mod. 7, mais si vous connaissez déjà cette notation, c'est qu'il n'y a plus rien à vous expliquer).
Pour ceux qui ne connaissent pas (Zn , +, ×) et qui voudraient tout de même savoir calculer sans passer plus d'une minute à apprendre.
Pour additionner ou multiplier dans Zn, faites exactement comme dans N ou Z, c'est tout ou presque :
si le résultat est aussi grand que n ou plus, divisez-le par n et donnez seulement le reste de la division.
Exemple pour n=5 :
On écrira pour simplifier, l'ensemble Z5 sous la forme Z5 = {0, 1, 2, 3, 4}.
Il n'y a pas d'élément 5 ni no plus au delà. 0 est mis à la place de tous les nombres {0, 5, 10, 15... }. De même 1 est à la place de {1, 6, 11, 16, ...} etc.
Calculez 2+2 = 4, 1+2 = 3 ... c'est simple, puis 3+4 = 12 que l'on écrira plutôt 2, on a donc 3+4 = 2, on a 1+4 = 0 etc. Il en est de même pour la multiplication : 3*4 = 2 (car en divisant 12 par 5, le reste est 2 ou si vous préférez, 12 = 5 + 5 + 2)
Autres exemples:
Dans Z7 6 × 5 = 30 et 30 divisé par 7 a pour reste 2, donc dans Z7 on a 6 × 5 = 2.
(C'est comme dans l'écriture 6 × 5 &equiv 2 mod. 7, mais si vous connaissez déjà cette notation, c'est qu'il n'y a plus rien à vous expliquer).
Documents - références - compléments - liens utiles
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


