Aire d'un ellipsoïde, formules approchées et nomogrammes
Ellipsoïde
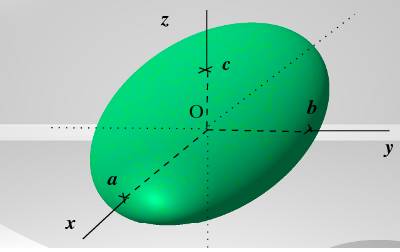
L'ellipsoïde de demi-axes $a$, $b$, $c$, ($ a>0, b>0, c>0 $), est la surface de $ \mathbb R^3 $ d'équation $ \displaystyle \frac {x^2} {a^2} + \frac {y^2} {b^2} + \frac {z^2} {c^2} = 1 $ .
Dans le cas général $ a > b > c $ l'ellipsoïde a la forme donnée sur l'image de synthèse ci-dessus (construite en s'aidant de POV-Ray, Xfig et Gimp, pour ne rien cacher).
Lorsque $ a=b=c=R>0 $, on obtient la sphère de rayon $R$ centrée à l'origine du repère (1ère image ci-dessous).
Lorsque deux seulement des demi-axes sont égaux (par exemple $ b=c $), le solide obtenu a encore un axe de révolution.
Si $ a> b=c $, (2ème image),l'ellipsoïde est allongé comme une olive ou un ballon de rugby, mais si $ a < b=c $, (3ème image ci-dessous), il est aplati comme certains comprimés de médicaments.



Le volume de la sphère de rayon $ R $ est $ \displaystyle V = \frac 4 3 \pi\,R^3 $, le volume de l'ellipsoïde de demi grands axes $ a $, $ b $, $ c $ est $ \displaystyle V = \frac 4 3 \pi\,a\,b\,c $
Aire d'un ellipsoïde
Pour $ c\leq b\leq a $ et en posant
$ \displaystyle\cos\varphi = \frac c a $,
$ \displaystyle k^2 = \frac{a^2(b^2-c^2)}{b^2(a^2-c^2)} $
et les intégrales elliptiques incomplètes de première espèce $ F( \varphi, k) $
et de deuxième espèce $ E( \varphi, k) $,
l'aire de l'ellipsoïde est
$ \displaystyle A = 2 \pi \left [ c^2 + \frac{ab}{\sin \varphi }\left ( E (\varphi, k)\sin^2\varphi + F(\varphi, k) \cos^2 \varphi \right ) \right ] $
où $ \cos \phi = \frac c a $, $ \displaystyle k^2 = \frac {a^2 (b^2-c^2)} {b^2(a^2-c^2)} $
(pour $ a > c $)
En compilant le programme Surface d'un ellipsoïde écrit en C, vous pourrez calculer l'aire S(a,b,c) d'un ellipsoïde. Ce programme utilise la bibliothèque GNU GSL de fonctions mathématiques.
Ce programme est utilisable en ligne à [Surface d'un ellipsoïde]. Indiquez les trois valeurs $ a $, $ b $ et $ c $ des demi-axes et le programme calculera la valeur exacte de l'aire de l'ellipsoïde.
Calcul approché de l'aire de l'ellipsoïde
Dans ce paragraphe on utilisera deux fonctions très différentes, la première donne une valeur
approchée à 0,65 % près et la seconde à 1.06 % près du résultat.
Lorsque le rapport entre la plus grande et la plus petite valeur des trois paramètres $a$, $b$, $c$ n'est pas trop grand, la précision, la précision est bien meilleure encore.
Les précisions 0.65 % et 1.06 % ont été déterminées expérimentalement en étudiant un grand nombre de cas, pour un rapport entre $a$, $b$ ou $c$ ne dépassant pas 1000.
Lorsque le rapport entre la plus grande et la plus petite valeur des trois paramètres $a$, $b$, $c$ n'est pas trop grand, la précision, la précision est bien meilleure encore.
Les précisions 0.65 % et 1.06 % ont été déterminées expérimentalement en étudiant un grand nombre de cas, pour un rapport entre $a$, $b$ ou $c$ ne dépassant pas 1000.
Calcul très simplifié mais moins précis de l'aire
Les résultats obtenus ci-dessous ne sont utilisables que pour des valeurs suffisamment proches les unes des autres de $a$, $b$ et $c$, sinon l'erreur relative peut rapidement dépasser 30 %. Le seul mérite de la formule est de permettre un calcul mental $ S \approx 4.2 (ab + bc + ca) $, ou à la rigueur $ 4 (ab + bc + ca) $.
Pour obtenir mentalement et rapidement une valeur approchée de l'aire, il suffit de calculer $ 4(ab+bc+ca) $ . Si vous remplacez $ 4 $ par $ 4,2 $ le calcul est plus compliqué, mais le résultat est meilleur.
Pour obtenir mentalement et rapidement une valeur approchée de l'aire, il suffit de calculer $ 4(ab+bc+ca) $ . Si vous remplacez $ 4 $ par $ 4,2 $ le calcul est plus compliqué, mais le résultat est meilleur.
Nomogrammes à axes parallèles
L'utilisation des nomogrammes
Vous pouvez télécharger et imprimer deux nomogrammes au format A4,
surfaceellipsoid30.pdf et
surfaceellipsoid100.pdf
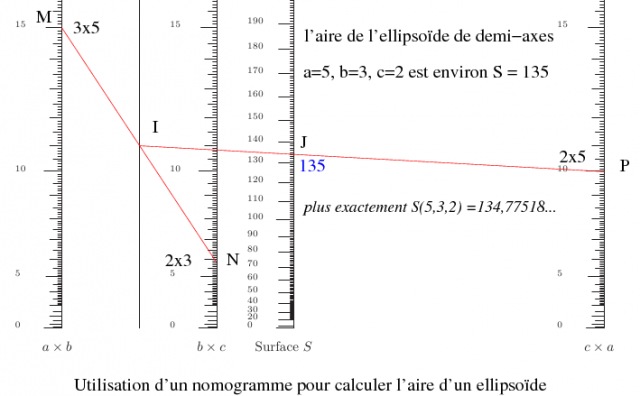
Un schéma explicatif ci-dessous montre comment utiliser les nomogrammes, mais auparavant il faut déjà avoir calculé les trois produits $ a\times b $, $ b\times c $ et $ c\times a $ des tois paramètres $ a $, $ b $, $ c $, deux à deux.
Pour obtenir ces trois produits on peut se servir d'une calculatrice, calculer mentalement ou se servir d'un nomogramme multiplicatif.
Un schéma explicatif ci-dessous montre comment utiliser les nomogrammes, mais auparavant il faut déjà avoir calculé les trois produits $ a\times b $, $ b\times c $ et $ c\times a $ des tois paramètres $ a $, $ b $, $ c $, deux à deux.
Pour obtenir ces trois produits on peut se servir d'une calculatrice, calculer mentalement ou se servir d'un nomogramme multiplicatif.

La construction du nomogramme
Un peu de géométrie dans un triangle
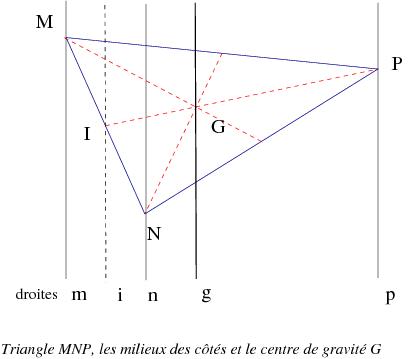
I, J et K sont les milieux des côtés du triangle MNP. Les médianes du triangle sont donc MJ, NK et PI, elles se coupent au centre de gravité G du triangle MNP.
Les droites parallèles fixes m, i, n, g et p passent par les points M, I, N, G, P.
Si on change les positions des sommets M, N, P du triangle sur les droites fixes m, n, p, alors le milieu I restera sur la droite i et le centre de gravité G restera aussi sur la droite fixe g.
Si dans un repère cartésien quelconque du plan, $ F $ est l'ordonnée du point G, $ X $ celle de M, $ Y $ celle de N et $ Z $ celle de P, alors $ 3 F = X + Y + Z $.
(Idem si $ F $, $ X $, $ Y $, $ Z $ sont les abscisses des points et non les ordonnées).
Une formule 3 F = X + Y + Z permet un nomogramme
L'excellente formule de Knud Thomsen donne la valeur approchée $\displaystyle S = 4\, \pi\, \left(\frac{a^pb^p + b^pc^p + c^pa^p} 3\right)^{\frac 1 p} $ où $ p = 1.6075 $. L'aire de l'ellipsoïde est obtenue avec une erreur relative ne dépassant pas $ 1.06 $%, ce qui est sans doute bien suffisant pour un nomogramme.
Il suffit d'écrire l'égalité sous la forme $ \displaystyle 3 \left(\frac{S}{4\,\pi}\:\right)^p = (ab)^p + (bc)^p + (ca)^p $ pour voir l'analogie entre cette formule et la formule précédente reliant les ordonnées des sommets du triangle MNP et du centre de gravité G. (G est l'isobarycentre des sommets M, n, P).
Ainsi donc, le point G d'ordonnée $ \displaystyle F = \left(\frac{S}{4\,\pi}\right)^p $ est l'isobarycentre de trois points M, N, P d'ordonnées $ \displaystyle X = (ab)^p $, $ \displaystyle Y = (bc)^p $
Il suffit d'écrire l'égalité sous la forme $ \displaystyle 3 \left(\frac{S}{4\,\pi}\:\right)^p = (ab)^p + (bc)^p + (ca)^p $ pour voir l'analogie entre cette formule et la formule précédente reliant les ordonnées des sommets du triangle MNP et du centre de gravité G. (G est l'isobarycentre des sommets M, n, P).
Ainsi donc, le point G d'ordonnée $ \displaystyle F = \left(\frac{S}{4\,\pi}\right)^p $ est l'isobarycentre de trois points M, N, P d'ordonnées $ \displaystyle X = (ab)^p $, $ \displaystyle Y = (bc)^p $

