Polynômes de couplage de Nn dans N - Partie I
Description
Les fonctions de couplages sont des bijections de $ \mathbb N^n $ vers $ \mathbb N $.
Les fonctions présentées dans cette page sont des polynômes de degré $ n $ en $ x = (x_1, x_2, \cdots , x_n) $, c'est-à-dire en $ n $ variables $x_1, x_2,\cdots, x_n $. Lorsque $ n = 2 $, on retrouve le polynôme de Cantor qui est une bijection de $ \mathbb N^2 $ vers $ \mathbb N $, dans le cas particulier $ n=2 $.
Toute permutation $ \sigma $ des variables $ x_1, x_2, \cdots , x_n $ permet d'obtenir une nouvelle fonction de couplage $ P $ $ \circ $ $ \sigma $, si $ P $ est un polynôme de degré $ n $, alors $ P $ $ \circ $ $ \sigma $ est aussi un polynôme de degré $ n $.
La première image représente la fonction de Cantor, l'image dans $ \mathbb N $ est indiquée en face du point de coordonnées $ (x_1, x_2) $ de $ \mathbb N^2 $.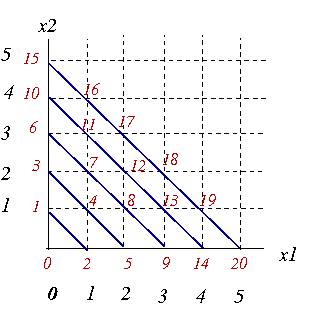
La deuxième image représente la fonction de Skolem de $ \mathbb N^3 $ vers $ \mathbb N $, seules quelques valeurs sont indiquées sur le schéma de gauche.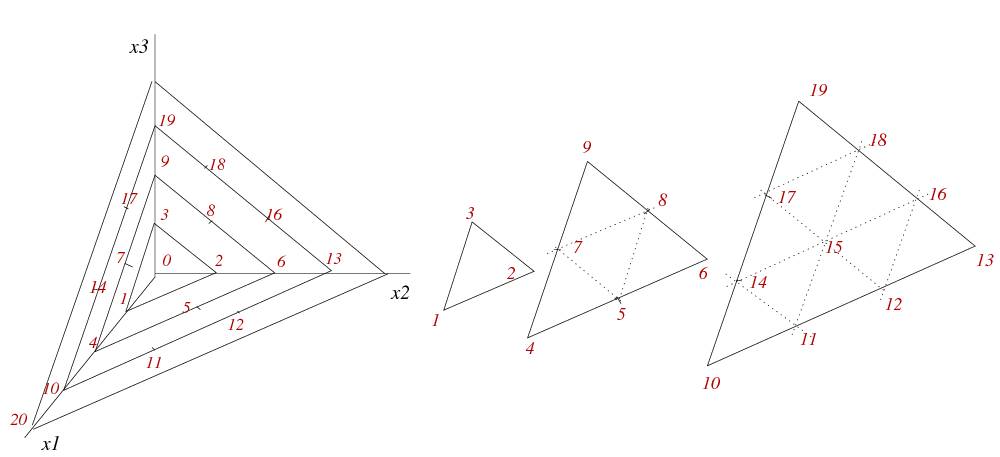
Les fonctions présentées dans cette page sont des polynômes de degré $ n $ en $ x = (x_1, x_2, \cdots , x_n) $, c'est-à-dire en $ n $ variables $x_1, x_2,\cdots, x_n $. Lorsque $ n = 2 $, on retrouve le polynôme de Cantor qui est une bijection de $ \mathbb N^2 $ vers $ \mathbb N $, dans le cas particulier $ n=2 $.
Toute permutation $ \sigma $ des variables $ x_1, x_2, \cdots , x_n $ permet d'obtenir une nouvelle fonction de couplage $ P $ $ \circ $ $ \sigma $, si $ P $ est un polynôme de degré $ n $, alors $ P $ $ \circ $ $ \sigma $ est aussi un polynôme de degré $ n $.
La première image représente la fonction de Cantor, l'image dans $ \mathbb N $ est indiquée en face du point de coordonnées $ (x_1, x_2) $ de $ \mathbb N^2 $.

La deuxième image représente la fonction de Skolem de $ \mathbb N^3 $ vers $ \mathbb N $, seules quelques valeurs sont indiquées sur le schéma de gauche.

Calculs de $ \mathbb N^n $ vers $ \mathbb N $ ou inversement
Décomposition en somme de $ y = P(x_1, x_2,\cdots,x_n) $ :
Polynômes de Skolem
Pour la même valeur de $ n $, l'application donne le polynôme de couplage de $ \mathbb N^n $ vers $ \mathbb N $.
Algorithmes
Plusieurs propriétés simples du triangle de Pascal du permettent d'obtenir les algorithmes élémentaires utilisés dans les applications qui précèdent, on obtient aussi l'expression du polynôme de Skolem.
Le tableau $ T = [T_{i,j}] $ ci-dessous est une partie du triangle de Pascal, ses éléments sont $ T_{i,j} = $ $ \binom{i+j-1}{i} $.
Ainsi l'image de $x = (x_1, x_2,\cdots,x_n) $ s'obtient en ajoutant les éléments du tableau $ T_{1,x_1}+T_{2,x_1+x_2}+T_{3,x_1+x_2+x_3}+\cdots $.
La décomposition en somme est indiquée par l'application ci-dessus après que vous ayez utilisé l'un des calculs ci-dessus, soit de $ x=(x_1, x_2,\cdots) $ vers $ P(x_1, x_2,\cdots)$, soit le calcul inverse .
Les termes de cette somme sont les éléments des cases du tableau dont le fond est colorié en orange, (lorsqu'ils ne sortent pas du cadre du tableau).
Le polynôme est donc $\displaystyle P(x_1,x_2,\ldots,x_n) = $ $\displaystyle T_{1,x_1}+ T_{2,x_1+x_2}+\cdots + T_{n,x_1+x_2+\cdots+x_n} = $ $\displaystyle \binom {x_1} 1 + \binom {x_1 + x_2 + 1} 2 +\cdots +\binom {x_1 + x_2 +\cdots+ x_n + n-1} n $.
Le tableau $ T = [T_{i,j}] $ ci-dessous est une partie du triangle de Pascal, ses éléments sont $ T_{i,j} = $ $ \binom{i+j-1}{i} $.
Ainsi l'image de $x = (x_1, x_2,\cdots,x_n) $ s'obtient en ajoutant les éléments du tableau $ T_{1,x_1}+T_{2,x_1+x_2}+T_{3,x_1+x_2+x_3}+\cdots $.
La décomposition en somme est indiquée par l'application ci-dessus après que vous ayez utilisé l'un des calculs ci-dessus, soit de $ x=(x_1, x_2,\cdots) $ vers $ P(x_1, x_2,\cdots)$, soit le calcul inverse .
Les termes de cette somme sont les éléments des cases du tableau dont le fond est colorié en orange, (lorsqu'ils ne sortent pas du cadre du tableau).
Le polynôme est donc $\displaystyle P(x_1,x_2,\ldots,x_n) = $ $\displaystyle T_{1,x_1}+ T_{2,x_1+x_2}+\cdots + T_{n,x_1+x_2+\cdots+x_n} = $ $\displaystyle \binom {x_1} 1 + \binom {x_1 + x_2 + 1} 2 +\cdots +\binom {x_1 + x_2 +\cdots+ x_n + n-1} n $.
| $ T_{i,j} $ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | $ 0 $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | $ 5 $ | $ 6 $ | $ 7 $ | $ 8 $ | $ 9 $ | $ 10 $ | $ 11 $ | $ 12 $ | $ 13 $ | $ 14 $ | $ 15 $ | $ 16 $ |
| 2 | $ 0 $ | $ 1 $ | $ 3 $ | $ 6 $ | $ 10 $ | $ 15 $ | $ 21 $ | $ 28 $ | $ 36 $ | $ 45 $ | $ 55 $ | $ 66 $ | $ 78 $ | $ 91 $ | $ 105 $ | $ 120 $ | $ 136 $ |
| 3 | $ 0 $ | $ 1 $ | $ 4 $ | $ 10 $ | $ 20 $ | $ 35 $ | $ 56 $ | $ 84 $ | $ 120 $ | $ 165 $ | $ 220 $ | $ 286 $ | $ 364 $ | $ 455 $ | $ 560 $ | $ 680 $ | $ 816 $ |
| 4 | $ 0 $ | $ 1 $ | $ 5 $ | $ 15 $ | $ 35 $ | $ 70 $ | $ 126 $ | $ 210 $ | $ 330 $ | $ 495 $ | $ 715 $ | $ 1001 $ | $ 1365 $ | $ 1820 $ | $ 2380 $ | $ 3060 $ | $ 3876 $ |
| 5 | $ 0 $ | $ 1 $ | $ 6 $ | $ 21 $ | $ 56 $ | $ 126 $ | $ 252 $ | $ 462 $ | $ 792 $ | $ 1287 $ | $ 2002 $ | $ 3003 $ | $ 4368 $ | $ 6188 $ | $ 8568 $ | $ 11628 $ | $ 15504 $ |
| 6 | $ 0 $ | $ 1 $ | $ 7 $ | $ 28 $ | $ 84 $ | $ 210 $ | $ 462 $ | $ 924 $ | $ 1716 $ | $ 3003 $ | $ 5005 $ | $ 8008 $ | $ 12376 $ | $ 18564 $ | $ 27132 $ | $ 38760 $ | $ 54264 $ |
| 7 | $ 0 $ | $ 1 $ | $ 8 $ | $ 36 $ | $ 120 $ | $ 330 $ | $ 792 $ | $ 1716 $ | $ 3432 $ | $ 6435 $ | $ 11440 $ | $ 19448 $ | $ 31824 $ | $ 50388 $ | $ 77520 $ | $ 116280 $ | $ 170544 $ |
| 8 | $ 0 $ | $ 1 $ | $ 9 $ | $ 45 $ | $ 165 $ | $ 495 $ | $ 1287 $ | $ 3003 $ | $ 6435 $ | $ 12870 $ | $ 24310 $ | $ 43758 $ | $ 75582 $ | $ 125970 $ | $ 203490 $ | $ 319770 $ | $ 490314 $ |
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


