Règles de Golomb
Pour construire une règle, cliquez sur les nombres de la longue liste bleue, au milieu de la page.
Ces règles graduées furent imaginées par le Dr. Solomon W. Golomb, professeur et chercheur intéressé par la théorie des nombres, la combinatoire, le codage et les communications et les jeux mathématiques.
Ces règles ont de nombreuses applications dans des domaines aussi variés que les radio communications, la cristallographie par rayons X, la théorie du codage, la radio astronomie.
Avant leur découverte par S. Golomb en théorie de l'information et du codage, elles sont utilisées dans un article de 1953 de W. Babcock pour réduire les effets d'intermodulation entre des canaux de fréquences radio, la méthode préconisée étant de placer les fréquences comme les marques d'une règle de Golomb. Babcock donne un tableau dans lequel les règles jusqu'à l'ordre 8 sont optimales.

Ces règles graduées furent imaginées par le Dr. Solomon W. Golomb, professeur et chercheur intéressé par la théorie des nombres, la combinatoire, le codage et les communications et les jeux mathématiques.
Ces règles ont de nombreuses applications dans des domaines aussi variés que les radio communications, la cristallographie par rayons X, la théorie du codage, la radio astronomie.
Avant leur découverte par S. Golomb en théorie de l'information et du codage, elles sont utilisées dans un article de 1953 de W. Babcock pour réduire les effets d'intermodulation entre des canaux de fréquences radio, la méthode préconisée étant de placer les fréquences comme les marques d'une règle de Golomb. Babcock donne un tableau dans lequel les règles jusqu'à l'ordre 8 sont optimales.
Description
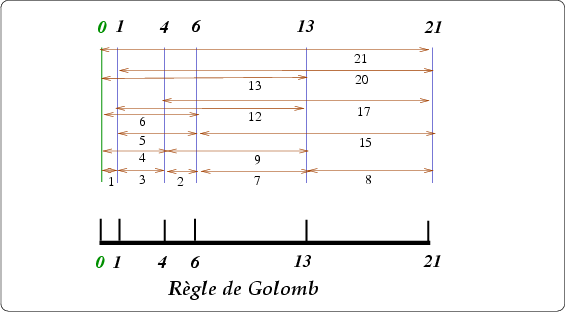
Sur la règle ci-dessus vous voyez six graduations 0, 1, 4, 6, 13, 21 qui permettent de mesurer 15 = 6×5/2 distances non nulles différentes 1, 2, 3, 4, 5, 7, 8, 9,..., 20, 21.
En regardant le schéma, vous pouvez retrouver toutes ces distances.
Vérifiez que vous ne trouvez entre deux graduations la même distance qu'entre deux autres graduationss. Ces conditions étant remplies, le nombre de graduations étant n, le nombre total de distances que l'on peut mesurer est n(n-1)/2. (Pour 6 graduations on obtient 15 différences non nulles)
Une règle de Golomb est un ensemble de marques (des points entiers d'un segment, les graduations), telles que les distances entre les paires de marques soient toutes différentes.
On convient que la première marque est 0 et que les autres sont positives.
En retournant une règle de Golomb (en inversant la droite et la gauche) on obtient une règle de Golomb. par exemple
Idéalement une règle de Golomb devrait permettre de mesurer toutes les distances entières de 0 jusqu'à la plus grande graduation. Quelques règles ont cette propriété, elles sont dites parfaites, mais elles ne sont pas nombreuses, 0 1 3 en est une, essayez d'en trouver d'autres.
La longueur d'une règle de Golomb est sa plus grande marque (la dernière graduation).
L'ordre d'une règle de Golomb est le nombre de ses marques (graduation 0 comprise).
Parmi toutes les règles de Golomb de même ordre, celles les plus courte est dite optimale.
Vérifiez que vous ne trouvez entre deux graduations la même distance qu'entre deux autres graduationss. Ces conditions étant remplies, le nombre de graduations étant n, le nombre total de distances que l'on peut mesurer est n(n-1)/2. (Pour 6 graduations on obtient 15 différences non nulles)
Une règle de Golomb est un ensemble de marques (des points entiers d'un segment, les graduations), telles que les distances entre les paires de marques soient toutes différentes.
On convient que la première marque est 0 et que les autres sont positives.
En retournant une règle de Golomb (en inversant la droite et la gauche) on obtient une règle de Golomb. par exemple
0 3 4 9 11 et 0 2 7 8 11. En effet 11-11=0, 11-9=2, 11-4=7, 11-3=8, 11-0=11.
Idéalement une règle de Golomb devrait permettre de mesurer toutes les distances entières de 0 jusqu'à la plus grande graduation. Quelques règles ont cette propriété, elles sont dites parfaites, mais elles ne sont pas nombreuses, 0 1 3 en est une, essayez d'en trouver d'autres.
La longueur d'une règle de Golomb est sa plus grande marque (la dernière graduation).
L'ordre d'une règle de Golomb est le nombre de ses marques (graduation 0 comprise).
Parmi toutes les règles de Golomb de même ordre, celles les plus courte est dite optimale.
Construisez une règle de Golomb : Choisissez dans la liste bleue et cliquez
Cliquez sur l'un des nombres en bleu pour le sélectionner comme graduation (resp. comme différence, selon le mode choisi). Continuez jusqu'à épuisement complet de cette liste bleue.
Les nombres choisis seront recopiés en vert dans la liste immédiatement au-dessus, ce sont les marques de la règle de Golomb (resp. les distances entre les marques consécutives)
(Attention, vous devrez choisir les graduations de plus en plus grandes. Si vous regrettez votre choix, cliquez sur le deuxième bouton)
Les nombres choisis seront recopiés en vert dans la liste immédiatement au-dessus, ce sont les marques de la règle de Golomb (resp. les distances entre les marques consécutives)
(Attention, vous devrez choisir les graduations de plus en plus grandes. Si vous regrettez votre choix, cliquez sur le deuxième bouton)
Marques / Écarts
Schéma de la règle
Choisissez la prochaine marque / ou l'écart
Cliquez l'un des nombres ci-dessous.
Distances entre marques consécutives
Triangle des différences
Les marques de la règle de Golomb se trouvent au-dessus du trait.
Les différences premières, entre deux marques consécutives, se trouvent sur la première ligne au-dessous du trait.
Les différences d'ordre k se trouvent sur la k-ième ligne sous le trait, ce sont les différences entre des marques dont les rangs diffèrent de k. Vous retrouvez ces deux éléments en suivant les diagonales montantes vers la gauche ou vers la droite, en partant de l'élément du tableau triangulaire.
(Attention : ce n'est pas un tableau de différences habituel, la deuxième ligne sous le trait peut être obtenue en additionnant la précédente ligne, pour les lignes suivantes c'est un peu plus compliqué).
Les différences premières, entre deux marques consécutives, se trouvent sur la première ligne au-dessous du trait.
Les différences d'ordre k se trouvent sur la k-ième ligne sous le trait, ce sont les différences entre des marques dont les rangs diffèrent de k. Vous retrouvez ces deux éléments en suivant les diagonales montantes vers la gauche ou vers la droite, en partant de l'élément du tableau triangulaire.
(Attention : ce n'est pas un tableau de différences habituel, la deuxième ligne sous le trait peut être obtenue en additionnant la précédente ligne, pour les lignes suivantes c'est un peu plus compliqué).
Défis
Défiez un ami ou vous-mêmes.
1) Essayez de trouver une règle la plus longue possible, se terminant par le nombre choisi (100 par exemple).
2) Essayez de trouver une règle de 7 marques non nulles dont la plus grande est 100. Essayez de trouver en 8 marques ou plus !
3) Essayez de trouver une règle la plus longue possible, dont la dernière marque est inférieure ou égale à 100, ou à 200 ...
4) Choisissez uniquement des marques dont le chiffre de droite est 5 (sauf pour la graduation initiale 0). Ou dont le chiffre de droite est 3 : 3 13 33 73 . Votre suite est-elle infinie ?
5) Essayez d'obtenir des écarts alternativement plus petits ou plus grands que le précédent : 6 - 5 - 10 - 9 - 13 - 12 - 16 - 1 - 39 - 23 - 31 - 26 - 7 - 69 - 27.
6) Recommencez avec d'autres containtes, par exemple en alternant des marques paires et des marques impaires. Ou uniquement des impairess (sauf le 0) : 1 3 7 15 25 41 61 91 123. Ou des multiples de 3. Ou des nombres premiers...
7) Construisez cette suite A101274 qui donne les écarts entre les graduations de 1 3 7 12 20 30 44 65 80 96 122 147 181 203 251. (Utilisez l'application ci-dessous pour automatiser les choix).
8) Essayez d'obtenir les écarts 1 2 4 8 10 16 20 30 32 48 44 en ne prenant que des graduations impaires
9) En jouant à deux, à tour de rôle, le premier qui joue avec un écart supérieur à 10 a perdu. Idem avec 20 ou un autre nombre fixé au départ. (Jeu de type Nim).
10) En jouant à deux, à tour de rôle, la graduation maximum à ne pas dépasser est : (la dernière jouée + 100)/2. Le premier à ne pas pouvoir jouer a perdu. (Jeu de type Nim).
11) Essayez d'approcher les règles optimales en utilisant l'application ci-dessous qui n'est relativement efficace que pour les règles de petites tailles.
1) Essayez de trouver une règle la plus longue possible, se terminant par le nombre choisi (100 par exemple).
2) Essayez de trouver une règle de 7 marques non nulles dont la plus grande est 100. Essayez de trouver en 8 marques ou plus !
3) Essayez de trouver une règle la plus longue possible, dont la dernière marque est inférieure ou égale à 100, ou à 200 ...
4) Choisissez uniquement des marques dont le chiffre de droite est 5 (sauf pour la graduation initiale 0). Ou dont le chiffre de droite est 3 : 3 13 33 73 . Votre suite est-elle infinie ?
5) Essayez d'obtenir des écarts alternativement plus petits ou plus grands que le précédent : 6 - 5 - 10 - 9 - 13 - 12 - 16 - 1 - 39 - 23 - 31 - 26 - 7 - 69 - 27.
6) Recommencez avec d'autres containtes, par exemple en alternant des marques paires et des marques impaires. Ou uniquement des impairess (sauf le 0) : 1 3 7 15 25 41 61 91 123. Ou des multiples de 3. Ou des nombres premiers...
7) Construisez cette suite A101274 qui donne les écarts entre les graduations de 1 3 7 12 20 30 44 65 80 96 122 147 181 203 251. (Utilisez l'application ci-dessous pour automatiser les choix).
8) Essayez d'obtenir les écarts 1 2 4 8 10 16 20 30 32 48 44 en ne prenant que des graduations impaires
9) En jouant à deux, à tour de rôle, le premier qui joue avec un écart supérieur à 10 a perdu. Idem avec 20 ou un autre nombre fixé au départ. (Jeu de type Nim).
10) En jouant à deux, à tour de rôle, la graduation maximum à ne pas dépasser est : (la dernière jouée + 100)/2. Le premier à ne pas pouvoir jouer a perdu. (Jeu de type Nim).
11) Essayez d'approcher les règles optimales en utilisant l'application ci-dessous qui n'est relativement efficace que pour les règles de petites tailles.
(Le record actuel pour n=25 de cette application est de 706
16 18 41 60 88 89 110 143 163 169 173 208 259 264 325 382 425 459 565 627 679 694 703 706 )
16 18 41 60 88 89 110 143 163 169 173 208 259 264 325 382 425 459 565 627 679 694 703 706 )
Documents - références - compléments - liens utiles
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


