Pi et Monte Carlo
Tirages aléatoires
 |
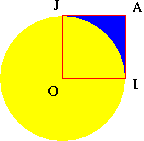Pi est évalué comme 4 fois le rapport du nombre de points situés dans le quart de disque (en haut à droite) au nombre total de points choisis dans le carré.
L'aire du quart de disque est Pi/4, celle du carré est 1. La probabilité qu'un point choisi au hasard dans le carré, se trouve dans le quart de disque est donc p = (Pi/4)/1 d'où Pi = 4p
Si on choisit N points au hasard dans le carré et si n de ces points sont dans le quart de disque, alors 4n/N est proche de Pi.
L'applet simule le choix des N points du carré et calcule la valeur approchée 4n/N de Pi.
(Vérifiez que votre navigateur permet l'utilisation de java et de javascript)
Simulations
Sources de PiMC.java
Pages de ce site, sur Pi
100000 décimales
Fréquences de sous-chaînes
Pi Quasi Monte Carlo
Calcul de 2 400 décimales de Pi Liens sur Pi
Calcul de 2 400 décimales de Pi Liens sur Pi
Liens
Pi et autres Yann Ollivier. Description d'une méthode n'utilisant que des nombres entiers
méthode de Monte-CarloMathématikos - site de Jean-Paul Quelen professeur de mathématiques au lycée Jean Monnet - Strasbourg
Relative Prime Applet the probability of two positive integers chosen at random being relatively prime is 6/(pi^2)
More java-links here
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.