1-Factorisations du graphe complet
La promenade des demoiselles
Tournoi par paires
Organisation
Le problème
Vous organisez un tournoi par paires entre n = 2p joueurs et vous voulez que chaque joueur rencontre une fois et une seule chacun des autres participants. Quelle sera la durée minimum du tournoi sachant que chaque joueur ne dispute pas plus d'un match par jour ?
Comme il y a p(2p-1) paires de deux joueurs et que l'on ne peut disputer que p matchs par jour, la durée sera au minimum de n-1 = 2p-1 jours.
(Lorsque le nombre réel de participants est impair, le concurrent 2p est fictif et évidemment ne jouera pas).
Comme il y a p(2p-1) paires de deux joueurs et que l'on ne peut disputer que p matchs par jour, la durée sera au minimum de n-1 = 2p-1 jours.
(Lorsque le nombre réel de participants est impair, le concurrent 2p est fictif et évidemment ne jouera pas).
Feuilles de rencontres
Il existe effectivement (au moins) une solution :
1) Entrez la liste des participants au tournoi (quel que soit leur nombre, pair ou impair).
2) Si vous voulez que la liste des noms soit brassée, cochez la case prévue à cet effet.
3) Cliquez sur le bouton [cherche]
4) Consultez les listes des rencontres
Pour retrouver la liste des noms, cliquez sur le bouton [Noms]
1) Entrez la liste des participants au tournoi (quel que soit leur nombre, pair ou impair).
2) Si vous voulez que la liste des noms soit brassée, cochez la case prévue à cet effet.
3) Cliquez sur le bouton [cherche]
4) Consultez les listes des rencontres
Pour retrouver la liste des noms, cliquez sur le bouton [Noms]
Exemples
Solution du problème simple
Origine : la promenade hebdomadaire des demoiselles
D'après C. Berge, le problème est celui de 'La promenade des demoiselles' (Lucas)
À cette époque - un siècle déjà - les n = 2*p demoiselles d'un pensionnat se promenaient tous les jours en rang par deux.
Le problème était de trouver comment les disposer pour qu'en n-1 = 2p-1 jours elles n'aient pas deux fois la même voisine.
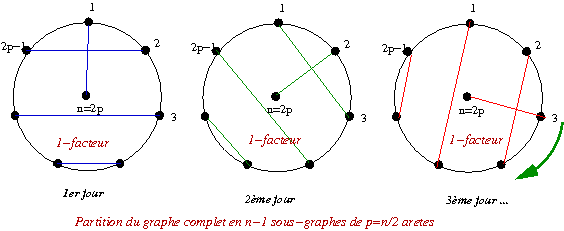
La solution de Lucas se retrouve aisément à partir du schéma ci-dessus.
Lorsque le nombre de demoiselle est impair, il suffit de compléter la liste par une demoiselle n = 2p fictive. (Chaque jour k, la demoiselle k est seule).
À cette époque - un siècle déjà - les n = 2*p demoiselles d'un pensionnat se promenaient tous les jours en rang par deux.
Le problème était de trouver comment les disposer pour qu'en n-1 = 2p-1 jours elles n'aient pas deux fois la même voisine.

La solution de Lucas se retrouve aisément à partir du schéma ci-dessus.
Lorsque le nombre de demoiselle est impair, il suffit de compléter la liste par une demoiselle n = 2p fictive. (Chaque jour k, la demoiselle k est seule).
Indice chromatique
L'indice chromatique d'un multigraphe sans boucles est le plus petit nombre de couleurs nécessaires pour colorier les arêtes, sachant que deux arêtes adjacentes (arêtes qui ont un sommet commun) ne peuvent être de même couleur.
Le problème des demoiselles se ramène à la recherche de l'indice chromatique d'un graphe complet K2n de n = 2p sommets.
Sur le double schéma (plus haut) les arêtes du 1er jour sont bleues, celle du 2ème jour sont vertes ... En utilisant n-1 couleurs et en superposant les n-1 cercles, on obtient bien un graphe complet (ci-dessous) et deux arêtes adjacentes de ce graphe ne sont jamais de la même couleur.
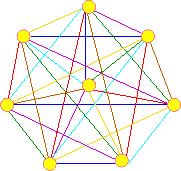
Graphe complet
Le problème des demoiselles se ramène à la recherche de l'indice chromatique d'un graphe complet K2n de n = 2p sommets.
Sur le double schéma (plus haut) les arêtes du 1er jour sont bleues, celle du 2ème jour sont vertes ... En utilisant n-1 couleurs et en superposant les n-1 cercles, on obtient bien un graphe complet (ci-dessous) et deux arêtes adjacentes de ce graphe ne sont jamais de la même couleur.

Graphe complet
1-Factorisations du graphe complet
Coloriage des arêtes et 1-Facteurs
Le problème se ramène à la recherche d'une partition de l'ensemble des arêtes du graphe, chaque partie correspond aux arêtes d'une même couleur. Les sous-graphes associés aux parties sont des 1-facteurs (chaque sommet est de degré 1).
Le graphe complet de n = 2p sommets a 2p-1 parties de p arêtes et 2p sommets.
Une recherche sur Google avec les mots "1-factorizations of the complete graph" est susceptible de fournir quelques adresses utiles.
Une recherche sur Google avec les mots "1-factorizations of the complete graph" est susceptible de fournir quelques adresses utiles.
Factorisations aléatoires
L'application ci-dessous effectue une recherche aléatoire d'une telle factorisation du graphe complet. Les résultats obtenus peuvent éventuellement, pour n = 2p égal ou supérieur à 8, donner des solutions non isomorphes entre elles.
Pour obtenir des résultats différents, cliquez à nouveau sur [Factorise], le bouton [P] ne cherche que les factorisations parfaites.
Pour obtenir des résultats différents, cliquez à nouveau sur [Factorise], le bouton [P] ne cherche que les factorisations parfaites.
Nombres de 1-factorisations
Pour obtenir toutes les solutions utilisez le programme C [ 1factorGComplet.c ] (utilisable à partir de n=4 sommets), qui donne 1 solution pour n=4, 6 solutions pour n=6,
6240 solutions pour n=8, 1225566720 pour n=10, ...
Jusqu'à n=8 les calculs sont immédiats, pour n=10 prévoir plusieurs heures de calculs (517m30.997s sur l'ordi utilisé), ensuite pour n=12 ce programme n'est plus assez rapide et ne vous donnera pas toutes les solutions.
Cette suite (1, 1, 1, 6, 6240, 1225566720, ...) est référencée A000438 dans EIS qui donne le terme suivant pour n=12 ainsi que des références.
Les nombres de solutions non-isomorphes sont donnés dans la suite EIS A000474.
Le programme minimise déjà le nombre de solutions en évitant les permutations des jours de tournois (la rencontre [0 - j] a lieu le jour j), on peut faire un peu mieux en fixant arbitrairement les tournois du premier jour : [0 - 1], [2 - 3] ... ce qui divise le nombre de solutions par A = n!/(p!*2^p) (en prenant p=n/2).
Jusqu'à n=8 les calculs sont immédiats, pour n=10 prévoir plusieurs heures de calculs (517m30.997s sur l'ordi utilisé), ensuite pour n=12 ce programme n'est plus assez rapide et ne vous donnera pas toutes les solutions.
Cette suite (1, 1, 1, 6, 6240, 1225566720, ...) est référencée A000438 dans EIS qui donne le terme suivant pour n=12 ainsi que des références.
Les nombres de solutions non-isomorphes sont donnés dans la suite EIS A000474.
Le programme minimise déjà le nombre de solutions en évitant les permutations des jours de tournois (la rencontre [0 - j] a lieu le jour j), on peut faire un peu mieux en fixant arbitrairement les tournois du premier jour : [0 - 1], [2 - 3] ... ce qui divise le nombre de solutions par A = n!/(p!*2^p) (en prenant p=n/2).
Types de 1-factorisations
Parfaites
Une conjecture de A. Kotzig
Les nombres de 1-factorizations parfaites (à une permutation près des 2p-1 facteurs), parmi celles dénombrées plus haut, sont a(p=1)=1, a(2)=1, a(3)=1, a(4)=960, a(p=5)=90720 ... (pour n=2p=2, 4, 6, 8, 10, ...)
L'existence de telles 1-factorisations parfaites est connue pour le graphe complet Kn=2p lorsque p ou 2p-1 sont premiers. Une liste d'entiers ne vérifiant pas ces deux conditions peut être obtenue ci-dessous en cliquant.
On connaît l'existence de 1-factorisations parfaites pour n = 2p = 16, 28, 36, 40, 50, 126, 170 et d'autres valeurs de la liste ci-dessus.
Voir la page de Jeffrey Dinitz
Sur le schéma ci-dessous à droite, la solution de Lucas ne conduit pas à une 1-factorisation parfaite (contre-exemple), toutefois n/2=5 est premier et une autre factorisation est parfaite.
En cliquant le bouton [P] de l'application précédente, vous lancez la recherche d'une 1-factorisation parfaite.
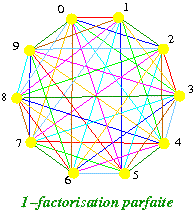

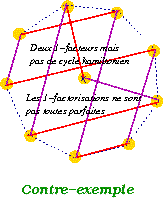
the perfect 1-factorization conjectureaffirme l'existence d'une 1-factorisation de tout graphe complet, telle que deux quelconques de ses 1-facteurs induisent toujours un cycle hamiltonien.
Les nombres de 1-factorizations parfaites (à une permutation près des 2p-1 facteurs), parmi celles dénombrées plus haut, sont a(p=1)=1, a(2)=1, a(3)=1, a(4)=960, a(p=5)=90720 ... (pour n=2p=2, 4, 6, 8, 10, ...)
L'existence de telles 1-factorisations parfaites est connue pour le graphe complet Kn=2p lorsque p ou 2p-1 sont premiers. Une liste d'entiers ne vérifiant pas ces deux conditions peut être obtenue ci-dessous en cliquant.
On connaît l'existence de 1-factorisations parfaites pour n = 2p = 16, 28, 36, 40, 50, 126, 170 et d'autres valeurs de la liste ci-dessus.
Voir la page de Jeffrey Dinitz
Handbook of Combinatorial Designs New Resultspour des précisions sur les résultats les plus récents.
Sur le schéma ci-dessous à droite, la solution de Lucas ne conduit pas à une 1-factorisation parfaite (contre-exemple), toutefois n/2=5 est premier et une autre factorisation est parfaite.
En cliquant le bouton [P] de l'application précédente, vous lancez la recherche d'une 1-factorisation parfaite.


Séquentiellement uniformes
Tous les sommets du sous-graphe formé par la réunion de deux 1-facteurs ont même degré 2 et ce sous-graphe est donc la réunion de plusieurs cycles dont les nombres de sommets (et aussi d'arêtes) ont pour somme n=2p. Dans le cas d'une 1-factorisation parfaite, toutes les réunions de deux facteurs n'ont qu'un seul cycle.
Lorsqu'on peut ordonner tous les 1-facteurs F0, F1,...,F2p-2 de telle manière que les unions de deux 1-facteurs consécutifs aient toutes des décompositions en cycles de mêmes longueurs, on dit que la 1-factorisation est séquentiellement uniforme.
En particulier, si les unions Fi et Fi+1 ont un seul cycle, la 1-factorisation est séquentiellement parfaite.
Lorsqu'on peut ordonner tous les 1-facteurs F0, F1,...,F2p-2 de telle manière que les unions de deux 1-facteurs consécutifs aient toutes des décompositions en cycles de mêmes longueurs, on dit que la 1-factorisation est séquentiellement uniforme.
En particulier, si les unions Fi et Fi+1 ont un seul cycle, la 1-factorisation est séquentiellement parfaite.
Uniformes
Lorsque toutes les unions de deux 1-facteurs différents Fi, Fj ont des cycles de mêmes longueurs, la 1-factorisation est dite uniforme.
Un certain nombre de 1-factorisations uniformes à partir de triples systèmes de Steiner sont connues .
Un certain nombre de 1-factorisations uniformes à partir de triples systèmes de Steiner sont connues .
Restrictions / Généralisations
Ajouts de contraintes
(Calendrier des rencontres, lieux.)
Un planning obtenu plus haut dans cette page permettra sans doute souvent l'organisation de tournois d'échecs (ou autres rencontres entre deux personnes), il risque d'être insuffisant si on désire programmer des rencontres d'équipes (commes celles de football, même en doublant chaque match aller par un match retour). Les contraintes dont il faudra tenir compte peuvent être nombreuses : disponibilité des lieux (terrains, salles) et des équipes à certaines dates (certaines équipes peuvent aussi participer à d'autres tournois), désir d'alterner pour chaque équipe les matchs sur son terrain et les match à l'extérieur ...
L'article (6) d'Andrea Schaerf, discute de ces problèmes et de méthodes de résolutions.
Un planning obtenu plus haut dans cette page permettra sans doute souvent l'organisation de tournois d'échecs (ou autres rencontres entre deux personnes), il risque d'être insuffisant si on désire programmer des rencontres d'équipes (commes celles de football, même en doublant chaque match aller par un match retour). Les contraintes dont il faudra tenir compte peuvent être nombreuses : disponibilité des lieux (terrains, salles) et des équipes à certaines dates (certaines équipes peuvent aussi participer à d'autres tournois), désir d'alterner pour chaque équipe les matchs sur son terrain et les match à l'extérieur ...
L'article (6) d'Andrea Schaerf, discute de ces problèmes et de méthodes de résolutions.
Problème des demoiselles de Kirkman
Contrairement à celles de Lucas, les quinze demoiselles de Kirkman se promènent en rang par trois. On veut que deux quelconques des filles se retrouvent une fois et une seule ensemble dans la même rangée de trois
Une solution est donnée dans le tableau ci-dessous. Chaque colonne correspond à une journée et les 15 demoiselles notées A, B, C ... M, N, O se retrouvent donc chaque jour en 5 sous-ensembles de trois filles (écrits et placés dans l'ordre alphabétique).
Une solution est donnée dans le tableau ci-dessous. Chaque colonne correspond à une journée et les 15 demoiselles notées A, B, C ... M, N, O se retrouvent donc chaque jour en 5 sous-ensembles de trois filles (écrits et placés dans l'ordre alphabétique).
| RANGS | Lun. | Mar. | Mer. | Jeu. | Ven. | Sam. | Dim. |
| 1 | ABC | ADH | AEM | AFI | AGL | AJN | AKO |
| 2 | DEF | BEK | BHN | BLO | BDJ | BIM | BFG |
| 3 | GHI | CIO | CGK | CHJ | CFM | CEL | CDN |
| 4 | JKL | FLN | DIL | DKM | EHO | DGO | EIJ |
| 5 | MNO | GJM | FJO | EGN | IKN | FHK | HLM |
Le nombre de paires de deux filles est de 15*14/2 = 105, or chaque groupe XYZ de trois filles correspond à trois paires XY YZ XZ, le nombre total de groupes distincts nécessaires, en supposant que le problème ait une solution, est donc de 105/3 = 35 (à choisir parmi les 15*14*13/6 = 35*13 =455 sous-ensembles possibles de trois filles).
Or chaque jour les 15 demoiselles sont réparties en 5 groupes de trois, il faudra donc une semaine entière pour réaliser les 35 = 7*5 groupes.
Or chaque jour les 15 demoiselles sont réparties en 5 groupes de trois, il faudra donc une semaine entière pour réaliser les 35 = 7*5 groupes.
Problème des "Golfeurs"
Le problème est de planifier m groupes de n golfeurs durant un certain nombre de semaines de telle manière qu'un golfeur ne se retrouve pas deux fois dans le même groupe que n'importe quel autre golfeur.
Un certain nombre de solutions sont présentées en (3) par Warwick Harvey.
Un certain nombre de solutions sont présentées en (3) par Warwick Harvey.
Le nombre total de golfeurs est n*m. Le nombre de paires est n*m*(n*m -1)/2.
Chaque groupe de n golfeurs correspond à n*(n-1)/2 paires et chaque semaine correspond à m*n*(n-1)/2 paires.
Le nombre de semaines qui permettrait d'épuiser toutes les paires de deux joueurs est donc
(n*m*(n*m -1)/2)/(m*n*(n-1)/2)=(n*m -1)/(n-1)=((n-1)*m+m -1)/(n-1)=m+(m-1)/(n-1) ce qui nous amène à prendre m de la forme m=1+k*(n-1) avec k= 0, 1, 2, ...
En faisant n=2 on retrouve le problème de Lucas : m=1, 2, 3, ... et le nombre de personnes est 2*m.
Avec m=5 et n=3 on a celui de Kirkman. Plus généralement pour n=3 les valeurs possibles de m sont les entiers impairs m = 1+2*k d'où un nombre de golfeurs égal à 3, 9, 15, 21, 27 ... lorsque des solutions existent
En prenant n=4 on a m=1+3*k d'où n*m= 4, 16, 28, 40, 52 ... lorsque des solutions existent
Avec m=5 et n=3 on a celui de Kirkman. Plus généralement pour n=3 les valeurs possibles de m sont les entiers impairs m = 1+2*k d'où un nombre de golfeurs égal à 3, 9, 15, 21, 27 ... lorsque des solutions existent
En prenant n=4 on a m=1+3*k d'où n*m= 4, 16, 28, 40, 52 ... lorsque des solutions existent
Problèmes apparentés ou extensions
Depuis la création de cette page sur les tournois par paires, Robert Ferréol a écrit le texte ci-dessous sur les tournois de plusieurs joueurs :
 Tournoi de Belote (PDF) (DOC) par Robert Ferréol professeur de mathématiques en mathématiques supérieures au lycée Carnot à Paris.
Tournoi de Belote (PDF) (DOC) par Robert Ferréol professeur de mathématiques en mathématiques supérieures au lycée Carnot à Paris.
D'autres groupes de quatre et un autre problème d'écoliers.
 Groupements par quatre, d'écoliers (PDF) Ma solution dans 'Taol Lagad' d'un problème posé il y a une trentaine d'années par un enseignant qui désirait répartir ses élèves par groupes de quatre. La résolution se fait par les carrés latins orthogonaux (les carrés bi-grécolatins). La construction effective de solutions utilise la théorie des groupes.
Groupements par quatre, d'écoliers (PDF) Ma solution dans 'Taol Lagad' d'un problème posé il y a une trentaine d'années par un enseignant qui désirait répartir ses élèves par groupes de quatre. La résolution se fait par les carrés latins orthogonaux (les carrés bi-grécolatins). La construction effective de solutions utilise la théorie des groupes.
Les suites de Skolem, les systèmes de différences et les systèmes triples de Steiner (non résolvables) à la page : Suites de Skolem. Notez qu'une suite de Skolem comme celle-ci
D'autres groupes de quatre et un autre problème d'écoliers.
Les suites de Skolem, les systèmes de différences et les systèmes triples de Steiner (non résolvables) à la page : Suites de Skolem. Notez qu'une suite de Skolem comme celle-ci
5 1 1 3 4 5 3 2 4 2 permet d'organiser un tournoi par paires en prenant pour premières rencontres les rangs
{0, 5}, {1, 2}, {3, 6}, {4, 8}, {7, 9} des éléments identiques de la suite de Skolem. Les jours suivants s'obtiennent ensuite par permutations circulaires.
Documentation, compléments, références
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


