Fibonacci's words and sequence
Leonardo Fibonacci
Biography
Fibonacci was born in Pisa about 1170. His father, a trader, settled then in the town of 'Bougie'(*) where Leonardo joined it.
Fibonacci studies the trade and mathematics by accomplishing many voyages in North Africa. Fibonacci takes note of work of the Arab mathematicians like Al Khwarizmi, learns numeration from Indian position. At the time, in Italy, the Roman numerals are still used and the 'zero' unknown.
Fibonacci studies the trade and mathematics by accomplishing many voyages in North Africa. Fibonacci takes note of work of the Arab mathematicians like Al Khwarizmi, learns numeration from Indian position. At the time, in Italy, the Roman numerals are still used and the 'zero' unknown.
Growth of a rabbit colony
The publication at the 13th century by Leonardo of Pisa (Fibonacci) of observations on the growth of a rabbit population is the origin of the sequence known as the Fibonacci's numbers.
At the beginning (t=0) there is a couple A of young rabbits
The next month (t=1) the two rabbits are adult, the couple A becomes B.
Obviously after a second month (t=2), two young rabbits are born and there are two couples : one couple B and one couple A.
Let us summarize: every month
The couples in the colony are, successively, A, B, BA, BAB, BABBA, BABBABAB... (they are the words of Fibonacci on the alphabet { A, B }).
The numbers of rabbit couples are (0), 1, 1, 2, 3, 5, 8... (numbers of Fibonacci).
At the beginning (t=0) there is a couple A of young rabbits
The next month (t=1) the two rabbits are adult, the couple A becomes B.
Obviously after a second month (t=2), two young rabbits are born and there are two couples : one couple B and one couple A.
Let us summarize: every month
- each A becomes B,
- each B becomes BA.
The couples in the colony are, successively, A, B, BA, BAB, BABBA, BABBABAB... (they are the words of Fibonacci on the alphabet { A, B }).
The numbers of rabbit couples are (0), 1, 1, 2, 3, 5, 8... (numbers of Fibonacci).
Words and numbers of Fibonacci
Definitions
The sequence (Fn) is defined by the initiating values F0=0, F1=1
and by the relation of recurrence Fn=Fn-1+Fn-2 for n>1.
The successive terms are
F0=0, F1=1, F2=1, F3=2, F4=3, F5=5, F6=8, F7=13, F8=21, F9=34, F10=55, F11=89, ...
To obtain Fn+1 one adds both Fn and Fn-1, for example F7=F6+F5=13+8=21.
In a similar way, we dfines the words of Fibonacci on the alphabet {0, 1}.
The successive words are given in the table below, the process of construction is indicated afterwards
The successive terms are
F0=0, F1=1, F2=1, F3=2, F4=3, F5=5, F6=8, F7=13, F8=21, F9=34, F10=55, F11=89, ...
To obtain Fn+1 one adds both Fn and Fn-1, for example F7=F6+F5=13+8=21.
In a similar way, we dfines the words of Fibonacci on the alphabet {0, 1}.
The successive words are given in the table below, the process of construction is indicated afterwards
| Range | Name | Word | Length | Number of '1' |
| 0 | M0 | {0} | 1 | 0 |
| 1 | M1 | {1} | 1 | 1 |
| 2 | M2 | {10} | 2 | 1 |
| 3 | M3 | {101} | 3 | 2 |
| 4 | M4 | {10110} | 5 | 3 |
| 5 | M5 | {10110101} | 8 | 5 |
| 6 | M6 | {1011010110110 } | 13 | 8 |
| n+1 | Mn+1 | MnMn-1 | Fn+1 = Fn + Fn-1 |
First method:
To obtain Mn+1 one write (joins) Mn and Mn-1, in this order.
For example M6 = M5 M4 ={10110101} {10110} = {1011010110110 }
To obtain Mn+1 one write (joins) Mn and Mn-1, in this order.
For example M6 = M5 M4 ={10110101} {10110} = {1011010110110 }
Calculation of the words of Fibonacci and the numbers
One uses the first method, described above.
Calculation using a morphism
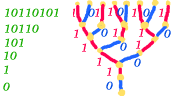 Second method:
Second method:
One can see indeed that this process is equivalent, while being simpler, with the morphism 0 -> 1, 1 -> 10 following:
to obtain Mn+1 replace in Mn
- all 0 by 1, (the young couples become old)
- all 1 by 10, (the old couples give rise to as many couples of young rabbits).
See also the page on morphisms, and the same example.
Listen to the air of music [Music] obtained while taking starting from each figure of the word of Fibonacci: (1)(0)(1)101011011010110101101101011011010110101... towards the line, the 7 binary characters successive (1)(0)(1)1010 (0)(1)10101 (1)101011... and by converting the numbers obtained 90 53 107(base 10) in notes
The script fib2midi uses Awk to produce the file fibonacci.abc in the 'abc' format which was then transformed into fibonacci.mid in the 'midi' format by the program abc2midi (a package of programs developed by James Allwright for processing ABC music notation files).
Programs
Lisp/Scheme
In the Scheme Scheme language : according to the book
Structure and interpretation of computer Programsby Harold Abelson/ Gerald Jay Sussman with Julie Sussman
1 ]=> (define (F n) (Fs n 1 0))
(define (Fs n s c)
(if (= n 0)
c
(Fs (- n 1) (+ s c) s)))
;Value: f
1 ]=>
;Value: fs
1 ]=> (F 3000)
41061588630797126033356837871926710522012510863736925240888543092690
55842741134037313304916608500445608300368357069422745885693621454765
02674373045446852160486606292497360503469773453733196887405847255290
08204908690751262205905454219588975803110922267084927479385953913331
83712447955431476110732762400667379340851917318109932017067768389347
66764778739502174470268627820918553842225858306408301661862900358266
85723821023580250435195147299791967652400478423637645334726836415264
83462458405732142414199379172429186026398100978669423920154046201538
18671425739835074851396421139982713640679581178458198658692285968043
243656709796000
Bc
The bc language accepts the equivalent program:
define fib(n) {
auto a, b, c, i;
a=0; b=1;
for(i=0;i<n;i++) {
c=a+b; a=b; b=c;
}
return(a);
}
print fib(3000), "\n";
quit;
Fast Javascript, online
Calculate in a few seconds, the hundreds or thousands figures of Fn
when n is large (n=1000 or n=10000 or even more).
The program uses the property:
For 0<= k<= n-2, F(n)=F(k+2)*F(n-k-1)+F(k+1)*F(n-k-2) who allows to calculate only one weak part of the numbers of Fibonacci preceding F(n).
hile taking k+1=50, nly are calculated two consecutive numbers of Fibonacci all the 50 positions.
The program is very simple to write and is approximately 25 times faster than with F(n)=F(n-1)+F(n-2). To design algorithms even faster for very great values of n, see for example my page of links on algorithms. If you installed Pari/Gp, you can try to calculate: fibonacci(10^6) and its 208988 digits.
Description Properties Applications.
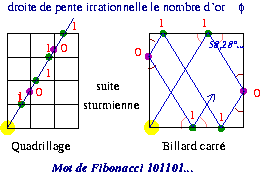
Word of Fibonacci on a grid and square billiards
 See the page on the genetic algorithms See the page on the genetic algorithms
(the genetics is used there to find the morphism 1->10, 0->1, by raising a population of words and does not have here strictly any relationship with the evolution of a rabbit colony). |
[Mus.] and [Mus.]
Cubes of Fibonacci
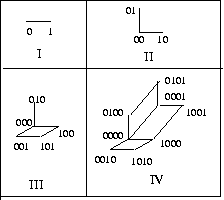
A cube of Fibonacci is the subgraph of a hypercube which one kept only the vertices whose binary code never has two digits 1 consecutive.
These vertices are given by the application below:
One can also build these graphs in the following way:
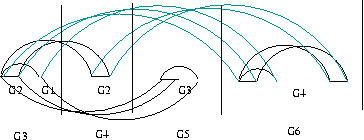
Gn+2 is obtained starting from Gn+1 and Gn by connecting the vertices of the two subgraphs Gn: the first in Gn+1 and the new one which is coupled with Gn+1.
Properties of the continuation of the numbers of Fibonacci
Linear recurrences
| Relations | Comments |
| F(n)= F(n-1)+F(n-2) | avec F(0)=0, F(1)=1 donne la définition |
| F(n)+F(n+3)=2 F(n+2) | F(n)+F(n+3) = F(n+2)-F(n+1) + F(n+2)+F(n+1) = 2 F(n+2) |
| F(n)+F(n+4)=3F(n+2) | ajouter F(n+4)-F(n+3)=F(n+2) à la précédente |
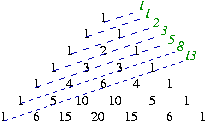
Number of paths
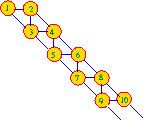 F(n) is the number of paths from box 1 to box N (allowed deplacements to right, bottom or both diagonally)
F(n) is the number of paths from box 1 to box N (allowed deplacements to right, bottom or both diagonally)
(1,2,4,5), (1,2,3,4,5), (1,2,3,5), (1,3,4,5), (1,3,5) are 5 paths allowing to arrive at '5' thus F(5) = 5. |
Fibonacci and the number 5
The emperor Frederic II, accompanied by his mathematicians Theodore and Jean of Palermo, had stopped in the town of Pisa in 1225 to meet Fibonacci whose fame was large and to organize a mathematical tournament. One of these questions was to find rational whose increased or decreased square by 5 is still a square. Fibonacci gave the solution 41/12. This amounts showing that 5 is a
congruent number and to find the right-angled triangle rational on sides c=9/6, b=40/6 and a=41/6 of surface 5.
The sequence of the congruent numbers is the A003273 sequence of N J. A. Sloane.
But obviously that has nothing to do with the number F(5) = 5 of the Fibonacci's sequence.
The sequence of the congruent numbers is the A003273 sequence of N J. A. Sloane.
But obviously that has nothing to do with the number F(5) = 5 of the Fibonacci's sequence.
Golden section
The linear relation of recurrence u(n)=u(n-1)+u(n-2) has for equation characteristic
x2=x+1 or x2 - x - 1 = 0 with
discriminant Delta = 5 and roots
a=(1-5½)/2 and b=(1+ 5½)/2 (b is the golden section)
There is thus a direct explicit formula
u(n) = A an + B bn
where A and B depend on u(0) and u(1).
The sequence of Fibonacci verify F(n) = (bn - an) / 5½
a=-0,618033988749894848... et b=1,618033988749894848...
|a| = 0,618... < 1 , implies that for n sufficiently large, F(n) is very close to
bn / 5½
Example : F(10) = 55 and b10 / 5½ = 55.0036361
The sequence or Fibonacci is close to a geometric sequence of reason b and
for n sufficiently large, F(n+1) is close to b×F(n)
Example : F(10) = 55, F(11) = 89 and b × F(10)=88.9918693
Development in continued fraction of the golden section
b= (1+ 5½)/2 verify b2 = b+1 thus
b = 1 + 1/b = 1+1/(1+1/b) = 1+1/(1+1/(1+1/b)) = ...
The golden section is approached by the successive quotients
Moreover, while dividing by F(n+1) the relation F(n+2) = F(n+1) + F(n), one obtains F(n+2) / F(n+1) = 1 + F(n) / F(n+1) or
Calculation of the terms Fn and the quotients of consecutive terms.
b = 1 + 1/b = 1+1/(1+1/b) = 1+1/(1+1/(1+1/b)) = ...
The golden section is approached by the successive quotients
|
Moreover, while dividing by F(n+1) the relation F(n+2) = F(n+1) + F(n), one obtains F(n+2) / F(n+1) = 1 + F(n) / F(n+1) or
|
Calculation of the terms Fn and the quotients of consecutive terms.
Sum of squares
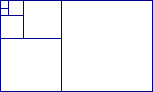
|
The figure explains the equality..
F2(0)+F2(1)+F2(2)+...+F2(n-1)+F2(n)=F(n)×F(n+1)
Demonstration by recurrence.
|
Triangles and Pi
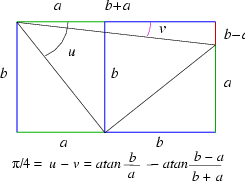
It is possible to take four consecutive Fibonacci numbers for b-a, a, b, b+a.
One obtains the Pi/4 relation Pi/4 = atan(Fn+1/Fn) - atan(Fn-1/Fn+2)
In particular with 3, 5, 8, 13, the relation is Pi/4 = atan(8/5) - atan(3/13).
But obviously one could also take numbers of Lucas (2,1,3,4,7,11,18,29...) or any nonnull sequence with the same linear recurrence u(n+1)=u(n)+u(n-1) such as for example 1, 7, 8, 15... and write Pi/4 = atan(8/7) - atan(1/15)
(What the formula gives when n -> infinity?)
Triangle of Pascal
Generating function and 'magical' inverses
By observing the decimal development of the inverses of 89, 9899, 998999, 99989999... and by inserting spaces, one reveals the first numbers of Fibonacci:
One obtains thus the six, eleven, sixteen, twenty... first numbers of Fibonacci.
When the numbers of Fibonacci have more figures than what is envisaged, they overflow and reserves come to modify the preceding sections. For this reason, only the first sections correspond to numbers of Fibonacci.
1/89 = 0. 0 1 1 2 3 5 955056...
1/9899 = 0.00 01 01 02 03 05 08 13 21 34 55 904636...
1/998999 = 0.000 001 001 002 003 005 008 013 021 034 055 089 144 233 377
610 9885...
1/99989999 = 0.0000 0001 0001 0002 0003 0005 0008 0013 0021 0034 0055
0089 0144 0233 0377 0610 0987 1597 2584 4181 67660947...
1/9999899999 = ...
One obtains thus the six, eleven, sixteen, twenty... first numbers of Fibonacci.
When the numbers of Fibonacci have more figures than what is envisaged, they overflow and reserves come to modify the preceding sections. For this reason, only the first sections correspond to numbers of Fibonacci.
x2 = F0x + (F1-F0)x2 + (F2-F1-F0)x3 +(F3-F2-F1)x4 +...
(car F0=0, F1=1 et Fn+2-Fn+1-Fn=0)
x2 = (1-x-x2)F0x + (1-x-x2)F1x2 + (1-x-x2)F2x3 + (1-x-x2)F3x4 +...
x2 = (1-x-x2) (F0x+F1x2+F2x3+F4x3+F4x5+... )
x2/(1-x-x2) = F0x+F1x2+F2x3+F4x3+F4x5+...
Replace x by 1/10 or 1/100 or 1/1000 ... (replace x-1 par 10, 100, 1000 ...) :
x2/(1-x-x2) = 1/(x-2-x-1-1)
= 1/(t2-t-1) with t = 1/x = 10,100, 1000, ...
Example :
aven:~\> echo "scale=150;1/9999899999"|bc .0000000001000010000200003000050000800013000210003400055000890014400\ 23300377006100098701597025840418106765109461771128657463687502621394\ 964211781614237
1) 1/89 2) 1/9899 3) 1/998999 4) 1/99989999 5) 1/9999899999 6) 1/999998999999
In the same manner we obtains the Lucas'sequence (N.J.A. Sloane A000032) verifyinh for n>=1, u(n+1)=u(n)+u(n-1) :
1) 19/89 2) 199/9899 3) 1999/998999 4) 19999/99989999 5) 199999/9999899999 6) 1999999/999998999999
Tribonacci (N.J.A. Sloane A000073) qui vérifie u(n+1)=u(n)+u(n-1)+u(n-2) à partir de n=2 :
1) 1/889 2) 1/989899 3) 1/998998999
Tetranacci (N.J.A. Sloane A000078) qui vérifie u(n+1)=u(n)+u(n-1)+u(n-2)+u(n-3) à partir de n=3 :
1) 1/8889 2) 1/98989899 3) 1/998998998999
Pisano's numbers
Giving the integer m>0, the sequence F(n) mod m is periodic A001175 by N. J. A. Sloane.
Periods of Fibonacci Sequence Modulo m et Find the Period of F(mod m) de Marc Renault,
Période du générateur de Fibonnaci Pierre L. Douillet les générateurs uniformes
Pisano Number by Eric Weisstein's World of Mathematics.
Periods of Fibonacci Sequence Modulo m et Find the Period of F(mod m) de Marc Renault,
Période du générateur de Fibonnaci Pierre L. Douillet les générateurs uniformes
Pisano Number by Eric Weisstein's World of Mathematics.
Bracelets
Fibonacci like sequences, modulo 10 :
The Number Bracelets Game - Susan Addington
How long (or short) a number bracelet can you make?
One wants to compose a bracelet of pearls chosen among 10 colors: c(0), c(1), c(2) = c(0)+c(1) modulo 10..., c(n+1) = c(n)+c(n-1).
After having determined one period, one makes a bracelet of it.
Which are the periods, the bracelets? Il s'agit de construire un bracelet de perles choisies parmi 10 couleurs : c(0), c(1), c(2) = c(0)+c(1) modulo 10, ..., c(n+1) = c(n)+c(n-1).
 On the figure, the modulo (and numbers of possible colors) is 11 and not 10. Can one build a bracelet of Fibonacci of 11 colors?
On the figure, the modulo (and numbers of possible colors) is 11 and not 10. Can one build a bracelet of Fibonacci of 11 colors?
While generalizing (the modulo n and the first two terms unspecified), one can seek to count the constructible bracelets by this same recurrence c(n+1) = c(n)+c(n-1).
The sequence A015134 of N. A. Sloane vive the numbers of periods of Fibonacci like sequences.
Below, one finds these values of this sequence and the various constructible bracelets:
One wants to compose a bracelet of pearls chosen among 10 colors: c(0), c(1), c(2) = c(0)+c(1) modulo 10..., c(n+1) = c(n)+c(n-1).
After having determined one period, one makes a bracelet of it.
Which are the periods, the bracelets? Il s'agit de construire un bracelet de perles choisies parmi 10 couleurs : c(0), c(1), c(2) = c(0)+c(1) modulo 10, ..., c(n+1) = c(n)+c(n-1).
 On the figure, the modulo (and numbers of possible colors) is 11 and not 10. Can one build a bracelet of Fibonacci of 11 colors?
On the figure, the modulo (and numbers of possible colors) is 11 and not 10. Can one build a bracelet of Fibonacci of 11 colors?
While generalizing (the modulo n and the first two terms unspecified), one can seek to count the constructible bracelets by this same recurrence c(n+1) = c(n)+c(n-1).
The sequence A015134 of N. A. Sloane vive the numbers of periods of Fibonacci like sequences.
Below, one finds these values of this sequence and the various constructible bracelets:
| Number of pearls in the bracelets | |
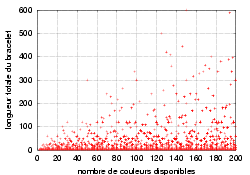
|
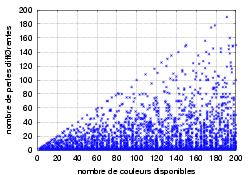
|
| total length of the bracelet | Distinct colors only |
to complete ...
Games
Fibonacci-Nim
At the beginning, the first player can eliminate all the matches except one.
Then, each player can withdraw until the double of the matches removed by the adversary at the preceding turn.
The winner is that which takes the last matches of the play.
Play the game here or at the page : Game of Fibonacci-Nim.
Then, each player can withdraw until the double of the matches removed by the adversary at the preceding turn.
The winner is that which takes the last matches of the play.
Play the game here or at the page : Game of Fibonacci-Nim.
Wythoff's game
game.
Zeckendorf's numeration
An alternative of a traditional game uses the numeration of Zeckendorf: each positive integer breaks up in a unique way into a sum of numbers of Fibonacci Fi (of ranges i>=2, differents, no consecutives).